19. Modelos de Mezcla de Gaussianas¶

19.1. Modelos de variable latente y clustering¶

Métodos no supervisados: Contrario a los modelos supervisados que vimos antes (regresión lineal, regresión logística), en el escenario no supervisado, no se tienen etiquetas o variable objetivo a ajustar.

El objetivo general de los métodos no-supervisados es revelar estructura en los datos y así facilitar su entendimiento.

Un ejemplo de lo anterior es la identificación de una causa oculta o variable latente. Este es el dominio de los modelos de variable latente (Latent Variable Models, LVM).

En un LVM se tiene la siguiente estructura:

Variable observada (efecto): Corresponde a nuestros datos.
Variable latente (causa): Una variable que busca explicar la variable observada.

Y en general el objetivo es: inferir la variable latente dada la variable observada. Para lo anterior asumimos alguna propiedad para la variable latente, por ejemplo:

La dimensión de la variable latente es menor que la de la variable observada: Métodos de reducción de dimensionalidad.
La variable latente es continua y tiene distribución Gaussiana: PCA.
Las variables latentes son independientes (la variable observada si puede estar correlacionada).

En esta lección nos enfocaremos en LVMs con variable latente discreta con aplicaciones para agrupamiento (clustering):

Clustering: Agrupar datos que sean “similares” en conjuntos (clusters)

Lo anterior requiere una definición de similitud.

19.2. Definición del modelo de mezcla¶

Un modelo de mezcla general es un LVM con variable discreta donde cada dato (variable observada) se representa como: $$ x_i \in \mathbb{R}^D \text{ with } i=1,\ldots, N $$

y tiene asociada una categoría discreta (variable latente):

\[ z_i \in {1, 2, \ldots, K}, \]

Podemos modelar el prior de $z_i$ como una distribución categórica:

\[ p(z_i) = \text{Cat}(\vec \pi), \]

donde $\pi_k \in [0, 1]$ son los coeficientes de mezcla y $\sum_{k=1}^K \pi_k=1$

Importante

Estamos asumiendo que existen $K$ conjuntos (clusters). La variable latente asociada a cada dato es uno entre los $K$ clusters.

Con lo anterior podemos escribir la verosimilitud del modelo de mezcla como:

(19.1)¶\[\begin{split} \begin{align} p(x_i | \theta) &= \sum_{k=1}^K p(x_i|z_i = k, \theta) p(z_i=k| \theta) \\ &= \sum_{k=1}^K p_k(x_i| \theta_k) \pi_k , \end{align} \end{split}\]

Para continuar debemos especificar una familia para $p_k(x_i|\theta_k)$.

Para el modelo de mezcla de gaussiana (Gaussian Mixture Model, GMM), asumiremos que cada componente de la mezcla sigue una distribución Gaussiana/normal.

Con lo anterior la Ecuación (19.1) queda como:

\[ p(x_i | \theta) = \sum_{k=1}^K \pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k), \]

donde cada cluster tiene tres parámetros:

La media del cluster $k$: $\mu_k$. Representa la ubicación del centro del cluster.
La covarianza del cluster $k$: $\Sigma_k$: Representa el tamaño y la orientación del cluster.
La concentración del cluster $k$: $\pi_k$: Representa la densidad del cluster.

Luego ajustar el GMM se redice a encontrar los mejores valores para estos parámetros para todos los clusters dado los datos

Nota

El GMM es un modeloge generativo, dado un valor para los parámetros podemos muestrar del GMM, generando datos nuevos.

Exploremos la influencia de estos parámetros a continuación con un ejemplo unidimensional y luego otro bidimensional. Asocie los valores de los parámetros con las gaussianas que observa en las figuras.

from utils import create_mixture

data, labels = create_mixture(pis=[0.4, 0.5, 0.1], 
                              mus=[[-1], [2], [2.5]], 
                              Sigmas=[0.1, 0.5, 0.1])

edges, bins = np.histogram(data, bins=50, density=True)

hv.Histogram((edges, bins), kdims='data', vdims='Density')

data, labels = create_mixture(pis=[0.9, 0.1], 
                              mus=[[-1, -1], [1, 1]], 
                              Sigmas=[0.5*np.eye(2), [[1, -0.9],[-0.9, 1]]])

bins, edgesx, edgesy = np.histogram2d(data[:, 0], data[:, 1], bins=30, density=True)

hv.Scatter((data[:, 0], data[:, 1])) +  hv.Image((edgesx, edgesy, bins))

19.2.1. Probabilidad a posteriori del GMM:¶

Asumiendo que conocemos los parámetros del GMM, una aplicación relevante es la de inferir el cluster más probable para un dato en particular,

Esto está dado por la probabilidad de $z$ dado $x$.

Utilizando la regla de Bayes y los supuestos previos podemos escribir:

(19.2)¶\[\begin{split} \begin{split} r_{ik} = p(z_i = k|x_i, \theta) &= \frac{ p(x_i|z_i = k, \theta) p(z_i=k| \theta)}{p(x_i)} \\ &= \frac{ p(x_i|z_i = k, \theta) p(z_i=k| \theta)}{ \sum_{k=1}^K p(x_i|z_i = k, \theta) p(z_i=k| \theta) } \\ &= \frac{ \mathcal{N}(x_i|\mu_k, \Sigma_k) \pi_k}{ \sum_{k=1}^K \mathcal{N}(x_i|\mu_k, \Sigma_k) \pi_k }, \end{split} \end{split}\]

este posterior también suele llamarse responsabilidad $r_{ik}$ del cluster $k$ para el dato $i$. Esto es lo que se conoce como una asignación de cluster suave (probabilidad de pertenecer a cada cluster)

En algunos casos sólo necesitamos una asignación de cluster fuerte, es decir descubrir cual es el cluster más probable:

\[ c_{i} = \text{arg}\max_k r_{ik} = \text{arg}\max_k \log \mathcal{N}(x_i|\mu_k, \Sigma_k) + \log \pi_k, \]

En cuyo caso podemos omitir la evidencia, es decir el denominador de la Ecuación (19.2).

La siguiente figura muestra la diferencia graficamente la diferencia entre una asignación suave y dura, en este caso para dos clusters.

def jointGMM(data, pi, mu, Sigma):
    # Assume 2 dimensional data
    data_centered = data - mu
    norm = pi/(2*np.pi*np.sqrt(np.linalg.det(Sigma)))
    xSx = np.multiply(data_centered, np.linalg.solve(Sigma, data_centered.T).T)
    return norm*np.exp(-0.5*np.sum(xSx, axis=1))

pis = [0.6, 0.4]; mus=[[-1, -1], [1, 1]]; 
Sigmas=[0.5*np.eye(2), [[1, -0.3],[-0.3, 1]]]
data, labels = create_mixture(pis, mus, Sigmas, rseed=0)

posterior = np.zeros(shape=(len(data), len(pis)))
for k in range(len(pis)):
    posterior[:, k] = jointGMM(data, pis[k], mus[k], Sigmas[k])
posterior = posterior/np.sum(posterior, axis=1)[:, np.newaxis]

p1 = hv.Scatter((data[:, 0], data[:, 1], posterior[:, 1]), 
                vdims=['y', 'z'], label='Soft assignment').opts(color='z')
p2 = hv.Scatter((data[:, 0], data[:, 1], np.argmax(posterior, axis=1)), 
                vdims=['y', 'z'], label='Hard assignment').opts(color='z')
hv.Layout([p1, p2]).cols(2).opts(hv.opts.Scatter(cmap='RdBu'))

19.2.2. Ajustando el GMM¶

Ajustar se refiere a encontrar los estimadores puntuales óptimos para el modelo estadístico.

Anteriormente aprendimos sobre el procedimiento de MLE. El logaritmo de la verosimilitud en este caso es:

\[ \log L(\pi,\mu,\Sigma) = \sum_{i=1}^N \log \sum_{k=1}^K \pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k) \]

Advertencia

Con la excepción de $K=1$, no se puede encontrar una expresión analítica para los valores óptimos de los parámetros.

En general cuando no tenemos datos completos, es decir cuando tenemos variables ocultas (latent) o perdidas (missing), el posterior no es sencillo de factorizar.

En este caso particular tenemos una variable latente $z_i$, la cual necesitamos marginalizar (sumar sobre $k$) para calcular la verosimilitud. En lo que sigue veremos un método de estimación aproximada conocido como Expectation Maximization (EM).

Algunos otros problemas del MLE/MAP para el caso de GMM:

No-convexo: muchos óptimos locales (Murphy 11.3.2)
Muy difícil de calcular, es NP-hard
Unidentifiability: Puede existir $K!$ configuraciones con exactamente la misma solución (label switching).
Singularidades: Un componente puede colapsar a un punto singular si $\Sigma \to 0$, provocando que $\log L \to \infty$

19.3. Método de Expectation Maximization (EM)¶

La solución de MLE requiere que podemos observar completamente los datos. Esto significa que

Conocemos $z_i$ para cada $x_i$, es decir que conocemos a cluster pertenece $x_i$

La log-verosimilitud completamente observada es:

\[ \log L_{\text{FO}}(\theta) = \sum_{i=1}^N \log p(z_i) p(x_i|z_i, \theta), \]

sin embargo en la práctica no conocemos $z$, por lo tanto la marginalizamos calculando el valor esperado dado el posterior:

\[\begin{split} \begin{split} Q(\theta, \theta^{\text{old}}) &= \mathbb{E}_{p(z|x, \theta^{\text{old}})} \left[\log L_{\text{FO}}(\theta) \right] \\ &= \sum_{k=1}^K \sum_{i=1}^N p(k|x_i, \theta^{\text{old}}) \log p(k) p(x_i|\theta_k), \end{split} \end{split}\]

que se conoce como la función auxiliar. Luego de esto actualizamos los parámetros del modelo maximizando:

\[ \theta^{\text{new}} = \text{arg}\max_\theta Q(\theta, \theta^{\text{old}}), \]

y finalmente asignamos

\[ \theta^{\text{old}} \leftarrow \theta^{\text{new}} \]

repitiendo este procedimiento hasta tener convergencia.

Este procedimiento iterativo:

Paso E: Estimar el valor esperado de la verosimilitud dado los parámetros actuales
Paso M: Maximizar el estimador y actualizar los parámetros

se llama Expectation Maximization (EM). EM es un algoritmo general:

puede utilizarse para resolver otros problemas sin solución analítica o con variables no observadas.
tiene muchas variantes: Incremental, Variacional, Monte-Carlo (Murphy 11.4.8 and 11.4.9)

19.3.1. Actualizaciones de EM para el caso de GMM¶

La función auxiliar para GMM sería:

\[\begin{split} \begin{split} Q(\theta, \theta^{\text{old}}) &= \sum_{k=1}^K \sum_{i=1}^N p(k|x_i, \theta^{\text{old}}) \log p(k) p(x_i|\theta_k) \\ &= \sum_{k=1}^K \sum_{i=1}^N r_{ik}^{\text{old}} \left(\log \pi_k + \log \mathcal{N}(x_i|\mu_k, \Sigma_k) \right) \end{split} \end{split}\]

donde $r_{ik}^{\text{old}}$ es la responsabilidad dado los parámetros de la iteración previa. Luego maximizamos $Q$ para actualizar los parámetros.

El estimador para las medias está dado por:

\[ \mu_{k}^{\text{new}} = \frac{1}{\sum_{i=1}^N r_{ik}^{\text{old}}} \sum_{i=1}^N r_{ik}^{\text{old}} x_i \]

El cual se obtiene de derivar $Q$ e igualarlo a cero.

Siguiendo el mismo procedimiento para la covarianza se llega a:

\[\begin{split} \begin{align} \Sigma_k^{\text{new}} &= \frac{1}{\sum_{i=1}^N r_{ik}^{\text{old}}} \sum_{i=1}^N r_{ik}^{\text{old}} (x_i - \mu_k) (x_i - \mu_k)^T \nonumber \\ &= -\mu_k \mu_k^T + \frac{1}{\sum_{i=1}^N r_{ik}^{\text{old}}} \sum_{i=1}^N r_{ik}^{\text{old}} x_i x_i^T \nonumber \end{align} \end{split}\]

Finalmente, incorporando la restricción $\sum_{k=1}^K \pi_k = 1$ se llega a:

\[ \pi_k^{\text{new}} = \frac{\sum_{i=1}^N r_{ik}^{\text{old}}}{N} \]

19.3.2. Resumen del algoritmo para ajustar GMM¶

(1) Inicializar (aleatoriamente) los centros de los clusters.
(2) Calcular la responsabilidad de los cluster para cada dato con:

\[ r_{ik}^{\text{old}} = \frac{ \mathcal{N}(x_i|\mu_k^{\text{old}}, \Sigma_k^{\text{old}}) \pi_k^{\text{old}}}{ \sum_{k=1}^K \mathcal{N}(x_i|\mu_k^{\text{old}}, \Sigma_k^{\text{old}}) \pi_k^{\text{old}} } \]

(3) Calcular los nuevos valores de los parámetros con:

\[ \mu_{k}^{\text{new}} = \frac{1}{\sum_{i=1}^N r_{ik}^{\text{old}}} \sum_{i=1}^N r_{ik}^{\text{old}} x_i, \]

\[ \Sigma_k^{\text{new}} = -\mu_k \mu_k^T + \frac{1}{\sum_{i=1}^N r_{ik}^{\text{old}}} \sum_{i=1}^N r_{ik}^{\text{old}} x_i x_i^T , \]

y

\[ \pi_k^{\text{new}} = \frac{\sum_{i=1}^N r_{ik}^{\text{old}}}{N} \]

(4) Actualizar los parámetros con $\theta^{\text{old}} \leftarrow \theta^{\text{new}}$.
(5) Si se cumple el criterio de convergencia entonces terminar, de lo contrario volver a 2.

19.3.3. Ejemplo usando los datos del “viejo fiel” (old faithful)¶

Iteración paso a paso (ref: Bishop Fig. 9.8)

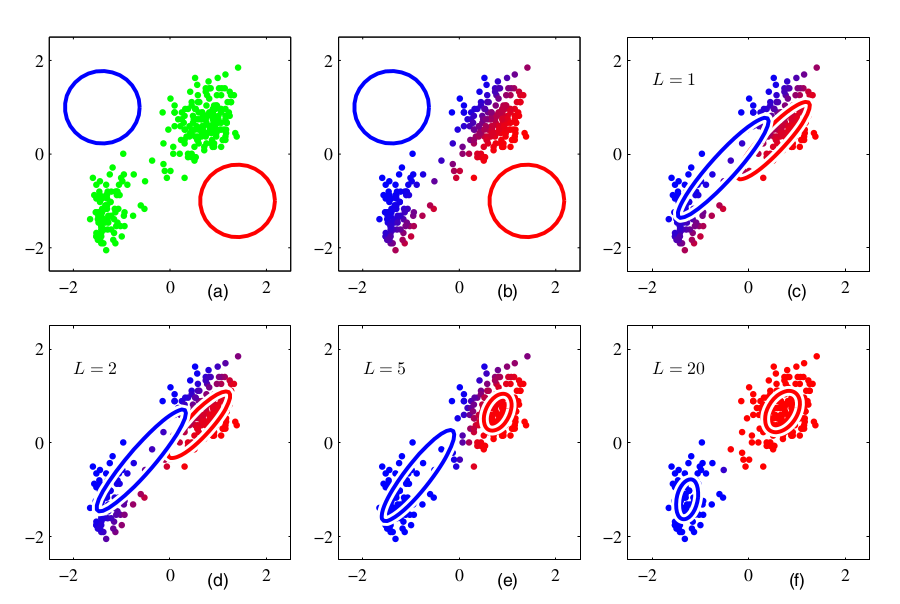
Animación obtenida de wikipedia:

https://upload.wikimedia.org/wikipedia/commons/6/69/EM_Clustering_of_Old_Faithful_data.gif

19.4. Detalles prácticos de EM:¶

Inicialización

El procedimiento de EM garantiza convergencia a un punto estacionario. Se puede obtener una mejor solución con la siguiente heurística:

Establecer una cierta “cantidad de reintentos”
Ejecutar GMM con inicialización aleatoria
Si la verosimilitud de la solución es mejor que la anterior entonces reemplazar, de lo contrario mantener la anterior
Repetir hasta que se cumpla la “cantidad de reintentos”

Otra heurística que mejora el desempeño es inicializar con la solución de un algoritmo más simple, como por ejemplo k-means. Esto puede evitar errores catastróficos pero también puede limitar la exploración.

Convergencia

EM es un procedimiento iterativo. ¿Cuántas veces repetimos el procedimiento?

Una heurística típica es detener el algoritmo si el logaritmo de la verosimilitud crece menos que un cierto valor porcentual con respecto al paso anterior (estancamiento).

Número de clusters

El número de clusters $K$ es un hiperparámetro que se escoje a priori por el usuario. ¿Cómo saber que valor de $K$ es adecuado?

Una opción es utilizar métricas que consideran tanto error como complejidad como por ejemplo

Criterio de información de Akaike (Akaike Information Criterion, AIC)
Criterio de información bayesiana (Bayesian Information Criterion, BIC)

\[ \text{BIC} = K \log N - 2 \log L \]

Una tercera opción es utilizar el coeficiente de silueata. Veremos algunos ejemplos de uso más adelante.

19.5. GMM con la librería `scikit-learn`¶

Del módulo sklearn.mixture tenemos la siguiente clase que implementa una mezcla de Gaussianas:

GaussianMixture(n_components=1, # Number of clusters
                covariance_type='full', # Shape of the covariance
                tol=0.001, # termination tolerance of EM
                max_iter=100, # Max number of EM iterations
                n_init=1, # Number of random initializations
                init_params='kmeans', # Initialization for the responsabilities (kmeans or random)
                ...
               )

donde el argumento covariance_type puede ser full, tied, diag o spherical.

En una covarianza diagonal $\Sigma = \vec \sigma^2 \text{I}$, $\vec \sigma \in \mathbb{R}_{+}^D$, los clusters no pueden tener rotaciones pero la varianza de cada dimensión puede ser diferente.
En una covarianza esférica $\Sigma = \sigma^2 \text{I}$, $\sigma \in \mathbb{R}_{+}$, los clusters no pueden tener rotaciones y todas las dimensiones tienen igual varianza.
Las covarianzas enlazadas (tied) significa que todos los clusters tienen la misma covarianza (comparten parámetros). Los clusters siguen tienen concentraciones y medias independientes.

Probemos el módulo utilizando datos sintéticos:

data, labels = create_mixture(pis=[0.33, 0.33, 0.34], 
                              mus=[[-3, 0], [0, 0], [3 ,0]], 
                              Sigmas=[[[1, 0.9],[0.9, 1]], 
                                      [[1, -0.9],[-0.9, 1]], 
                                      [[1, 0.9],[0.9, 1]]])

hv.Scatter((data[:, 0], data[:, 1])).opts(width=500)

Utilizaremos el BIC para encontrar el “mejor” número de clusters.

Para ajustar el modelo utilizamos el método fit
Para calcular el BIC utilizamos el método bic

from sklearn.mixture import GaussianMixture

maxK = 20; 
cov = 'full' 
metrics = np.zeros(shape=(maxK, ))
for i, K in enumerate(range(1, maxK+1)):
    gmm = GaussianMixture(n_components=K, covariance_type=cov, n_init=3)
    gmm.fit(data)
    metrics[i] = gmm.bic(data)

hv.Scatter((range(1, maxK+1), metrics), 'K', 'BIC').opts(size=10, width=500)

El BIC disminuye mientras más simple es el modelo y mientras mayor sea su log-verosimilitud. El mejor modelo es aquel que tiene menor BIC.

En este caso el mínimo BIC se obtiene con $K=3$. Utilicemos este valor e inspeccionemos los resultados

Utilizamos el método predict para obtener las predicciones duras (asignaciones)
Utilizamos el método predict_proba para obtener las predicciones suaves (probabilidades)

gmm = GaussianMixture(n_components=3, covariance_type=cov, n_init=3)
gmm.fit(data)
hatr = gmm.predict(data)

The hard assignments:

hv.Scatter((data[:, 0], data[:, 1], hatr), vdims=['y', 'z'],).opts(width=500, color='z', cmap='Category10')

Con las predicciones probabilísticas podemos calcular la entropía de Shannon:

\[ H = -\sum p_i \log p_i \]

p = gmm.predict_proba(data)
H = -np.sum(p*np.log(p), axis=1)

hv.Scatter((data[:, 0], data[:, 1], H), vdims=['y', 'z'],).opts(width=500, color='z', cmap='Blues', colorbar=True)

Mientras mayor sea la entropía (color más azul) mayor es la incertidumbre respecto a cual cluster pertenece el dato.

Finalmente podemos utilizar el método sample para generar datos sintéticos con el modelo

hatdata = gmm.sample(n_samples=10000)
hatdata

(array([[ 2.06340828, -1.07007695],
        [ 2.86170661,  0.10709019],
        [ 3.25894392,  0.08142743],
        ...,
        [-1.75787252,  1.93051828],
        [-2.03886209,  1.51653256],
        [-0.24115727, -0.03886263]]),
 array([0, 0, 0, ..., 2, 2, 2]))

hv.Scatter((hatdata[0][:, 0], hatdata[0][:, 1])).opts(width=500)

19.6. Apéndice¶

Relación con el algoritmo de K-means

El algoritmo K-means es un caso particular de GMM con las siguientes restricciones:

Clusters con covarianza esférica: $\Sigma = \sigma^2 \text{I}$, $\sigma \in \mathbb{R}_{+}$
Clusters con igual varianza: $\sigma^2 = \sigma_1^2 = \sigma_2^2 = \ldots = \sigma_K^2$
Prior uniforme para la concentración de los clusters: $\pi_k = \frac{1}{K}$
Se usan siempre asignaciones duras en lugar de probabilísticas

Con lo anterior la regla de actualización de la responsabilidad se reduce a:

\[\begin{split} \begin{split} \hat r_{ik}^{\text{old}} &= \text{arg} \max_k \frac{ \exp \left(-\frac{1}{2\sigma^2} \|x_i - \mu_k\|^2 \right) }{ \sum_{k=1}^K \exp \left(-\frac{1}{2\sigma^2} \|x_i - \mu_k\|^2 \right) } \\ &= \text{arg} \max_k \log \exp \left(-\frac{1}{2\sigma^2} \|x_i - \mu_k\|^2 \right) \\ &= \text{arg} \min_k \frac{1}{2\sigma^2} \|x_i - \mu_k\|^2 \\ &= \text{arg} \min_k \|x_i - \mu_k\|^2 \end{split} \end{split}\]

Y el único parámetro que es necesario actualizar son las medias de los clusters:

\[ \mu_{k}^{\text{new}} = \frac{1}{\sum_{i=1}^N \hat r_{ik}^{\text{old}}} \sum_{i=1}^N \hat r_{ik}^{\text{old}} x_i \]

Y estas se aplican iterativamente al igual que el con el método de EM.

Material adicional y referencias

Puede profundizar revisando el capítulo 11 del libro “Machine Learning: A Probabilistic Perspective”, de Kevin Murphy.
El siguiente artículo de scikit-learn explica como se puede ajustar el hiperparámetro de concentración del prior

Herramientas estadísticas para la investigación

Modelos de Mezcla de Gaussianas

Contenido

19. Modelos de Mezcla de Gaussianas¶

19.1. Modelos de variable latente y clustering¶

19.2. Definición del modelo de mezcla¶

19.2.1. Probabilidad a posteriori del GMM:¶

19.2.2. Ajustando el GMM¶

19.3. Método de Expectation Maximization (EM)¶

19.3.1. Actualizaciones de EM para el caso de GMM¶

19.3.2. Resumen del algoritmo para ajustar GMM¶

19.3.3. Ejemplo usando los datos del “viejo fiel” (old faithful)¶

19.4. Detalles prácticos de EM:¶

19.5. GMM con la librería `scikit-learn`¶

19.6. Apéndice¶

Herramientas estadísticas para la investigación

Modelos de Mezcla de Gaussianas

Contenido

19. Modelos de Mezcla de Gaussianas¶

19.1. Modelos de variable latente y clustering¶

19.2. Definición del modelo de mezcla¶

19.2.1. Probabilidad a posteriori del GMM:¶

19.2.2. Ajustando el GMM¶

19.3. Método de Expectation Maximization (EM)¶

19.3.1. Actualizaciones de EM para el caso de GMM¶

19.3.2. Resumen del algoritmo para ajustar GMM¶

19.3.3. Ejemplo usando los datos del “viejo fiel” (old faithful)¶

19.4. Detalles prácticos de EM:¶

19.5. GMM con la librería scikit-learn¶

19.6. Apéndice¶

19.5. GMM con la librería `scikit-learn`¶