Modelamiento con métodos no-paramétricos
Contenido
import holoviews as hv
hv.extension('bokeh')
import numpy as np
import scipy.signal
8. Modelamiento con métodos no-paramétricos¶
En esta lección revisaremos dos métodos no-paramétricos de modelamiento, los histogramas y la estimación de densidad por kernels (Kernel Density Estimation, KDE).
Estos métodos no-paramétricos nos permiten modelar distribuciones arbitrarias, es decir distribuciones cuya forma funcional no es conocida a priori.
Por lo anterior, estos métodos son ideales para procesos de exploración, donde buscamos estudiar las características estadísticas de nuestros datos. Nuestras observaciones luego puede ser insumo para proponer modelos paramétricos (estructura conocida a priori) más robustos.
8.1. El Histograma¶
Un histograma es una representación aproximada de una distribución de datos numérica. Esta aproximación se realiza utilizando el concepto de frecuencia (conteo). En su forma más simple la construcción de un histograma tiene tres pasos
Establecer un rango para el histograma: valor mínimo y máximo
Dividir el rango en un cierto número de particiones (bins)
Medir la frecuencia relativa en cada bin, es decir la cantidad de datos que caen en dicho bin
Luego la frecuencia se grafica utilizando barras.
Ejemplo: Para construir el siguiente histograma se utilizaron \(7\) bines de tamaño \(1\) regularmente distribuidos en el rango \([-3,4]\)
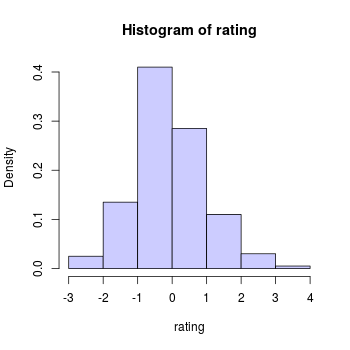
La principal utilidad del histograma es exploración de las propiedades estadísticos de nuestros datos. En base al histograma podemos extraer información acerca de:
La cantidad de modas
La localización (media) y ancho (varianza) de las modas
La diferencia relativa entre las colas de cada moda (simetría)
entre otras. Del ejemplo anterior podemos ver que la distribución es unimodal, con ubicación cercana (aunque ligeramente inferior) a cero y con una ligera asimetría de colas.
Prudencia
La cantidad de particiones (bines) utilizados para construir el histograma afecta de forma importante nuestras observaciones. Conviene probar con distintos valores de este hiperparámetro y comparar. Más adelante ahondaremos en este punto.
Nota
El ejemplo anterior corresponde al caso particular más común donde los cajones son disjuntos y de igual tamaño. Otros métodos como, Bayesian blocks puede utilizarse para construir histogramas con particiones de tamaño variable
8.1.1. Histograma con Python¶
Utilizando la librería Numpy podemos utilizar
numpy.histogram(a, # arreglo (unidimensional) de datos
bins=10, # Números de particiones (cajones) o un arreglo con los límites de las mismas
range=None, # Tupla con valor inicial y final
density=None, # Si es True entonces retorna densidades (frecuencia relativa)
...
)
que retorna una tupla con dos arreglos: los bordes de las particiones y las frecuencias (o densidades) de las particiones. Veamos un ejemplo:
from dists import GaussianMixture
# Generación de los datos
dist = GaussianMixture(locs=[-4, 3], scales=[2, 2], weights=[0.7, 0.3])
samples = dist.rvs(1000, seed=1234)
x = np.linspace(np.amin(samples), np.amax(samples), num=1000)
pdf = dist.pdf(x)
# Construcción de histogramas con distintas particiones e igual rango
histograms = {}
for nbins in [1, 2, 5, 10, 20, 50, 100]:
histograms[nbins] = np.histogram(samples, bins=nbins,
range=(np.amin(samples), np.amax(samples)),
density=True)
A continuación se muestra el histograma de las muestras con la distribución subyacente de fondo.
Utiliza el control deslizante para estudiar la influencia del número de particiones (bins):
dist_plot = hv.Curve((x, pdf)).opts(line_width=2, color='k', width=500, height=350)
hmap = hv.HoloMap(kdims='Number of bins')
for key, (freqs, bins) in histograms.items():
hmap[key] = hv.Histogram((bins, freqs), kdims='x', vdims='Density').opts(alpha=0.75)
hmap * dist_plot
Nota
En general
Un número muy pequeño de bins “pierde” las características de la distribución, por ejemplo la multimodalidad
Un número muy grande de bins introduce ruido que dificulta la lectura del histograma
8.1.2. ¿Cómo seleccionar el número de particiones?¶
Este hiperparamétro puede seleccionar haciendo una validación cruzada sobre nuestros datos. Una métrica ampliamente utilizada para lo anterior es el error cuadrático medio asintótico (Asymptotic Mean Integrated Square Error, AMISE)
También existen algunas “reglas del dedo” (rules of thumb), que suelen ser adecuadas como punto de partida. Dos ejemplos son la regla de Scott y la regla de Silverman. Ambas
son proporcionales con la dispersión de los datos e inversamente proporcional con la cantidad de muestras
se obtienen de imponer supuestos sobre la distribución subyacente de los datos
Por ejemplo la regla de Silverman para el ancho de las particiones es:
donde \(N\) es el número de observaciones, \(\sigma\) es la desviación estándar y \(q_{75}-q_{25}\) es el rango intercuartil. Luego usando este ancho podemos calcular el número de particiones con:
Prudencia
La regla de Silverman es óptima sólo si la distribución subyacente es Normal (Gaussiana). En caso general puede servir como punto de partida.
8.2. Kernel density estimation (KDE)¶
KDE puede considerarse como una alternativa al histograma donde cada muestra es su “propia partición”, y donde las particiones pueden solaparse. Debido a lo anterior no se requiere escoger los límites de las particiones, sólo su ancho.
La distribución unidimensioanl aproximada con KDE para una muestra \(\{x_i\}_{i=1,\ldots, N}\) es
donde \(h\) se llama ancho de banda de kernel (kernel bandwidth) y \(\kappa(u)\) es una función de kernel que debe ser positiva, con media cero y además integrar a la unidad.
Por ejemplo, un kernel muy utilizado es:
que se conoce como kernel Gaussiano. Otros kernels ampliamente utilizados en KDE son el kernel de Epanechnikov y el kernel Top-hat
Prudencia
Utilizar un kernel Gaussiano no implica a sumir que los datos se distribuyan Gaussianos (normales). Es totalmente correcto utilizar un kernel Gaussiano en datos no-Gaussianos
8.2.1. KDE en Python¶
KDE está implementado en el módulo sklearn.neighbors como
KernelDensity(kernel='gaussian', # kernel
bandwidth=1.0, # ancho
...
)
Sus métodos más importantes son
fit(xi: np.ndarray): Guarda las muestras que se utilizarán para calcular las densidadesscore_samples(x: np.ndarray): Returna un arreglo de numpy con el logaritmo de las densidades evaluadas en el arreglox
A continuación se la estimación con kernels de la distribución del ejemplo anterior:
from sklearn.neighbors import KernelDensity
hs = 0.9*np.std(samples)*len(samples)**(-1/5)
densities = {}
for k in [1/8, 1/4, 1/2, 1, 2, 4, 8]:
for kernel in ["gaussian", "epanechnikov", "tophat"]:
kde = KernelDensity(kernel=kernel, bandwidth=hs*k).fit(samples.reshape(-1, 1))
densities[k, kernel] = np.exp(kde.score_samples(x.reshape(-1, 1)))
Utiliza el control deslizante para estudiar la influencia de la función de kernel y de su ancho (indicado en k veces el ancho de Silverman)
dist_plot = hv.Curve((x, pdf)).opts(line_width=2, color='k', width=500, height=350)
hmap = hv.HoloMap(kdims=['Width/Silverman', 'Kernel'])
for key, density in densities.items():
hmap[key] = hv.Curve((x, density), kdims='x', vdims='Density').opts(line_width=2)
hmap * dist_plot
Nota
En general
Un ancho grande las características de la distribución
Un ancho pequeño introduce ruido
