Variables aleatorias especiales
Contenido
4. Variables aleatorias especiales¶
Existen algunos tipos de variables aleatorias especiales, definidas por que tienen distribuciones de probabilidad particulares.
4.1. Distribución Bernoulli¶
Suponga que se realiza un ensayo cuya salida es “éxito” o “falla”. La v.a. entonces tiene sólo dos valores posibles: 1 si “éxito” 0 si no. Si \(p\) es la probabilidad de éxito, entonces:
\(\begin{array}{lll} P(X=1) & = &p \qquad y \qquad P(X=0) = 1-p \\ P(X = i) & = & p^i (1-p)^i \,, i=0,1\\ E[X] & = & p\\ Var(X) & = & p(1-p)\\ Asimetria(X) & = & \frac{1-2p}{\sqrt{p(1-p)}}\\ Curtosis(X) & = & \frac{1-3p+3p^2}{p(1-p)}\\ \end{array}\)
4.2. Distribución Binomial¶
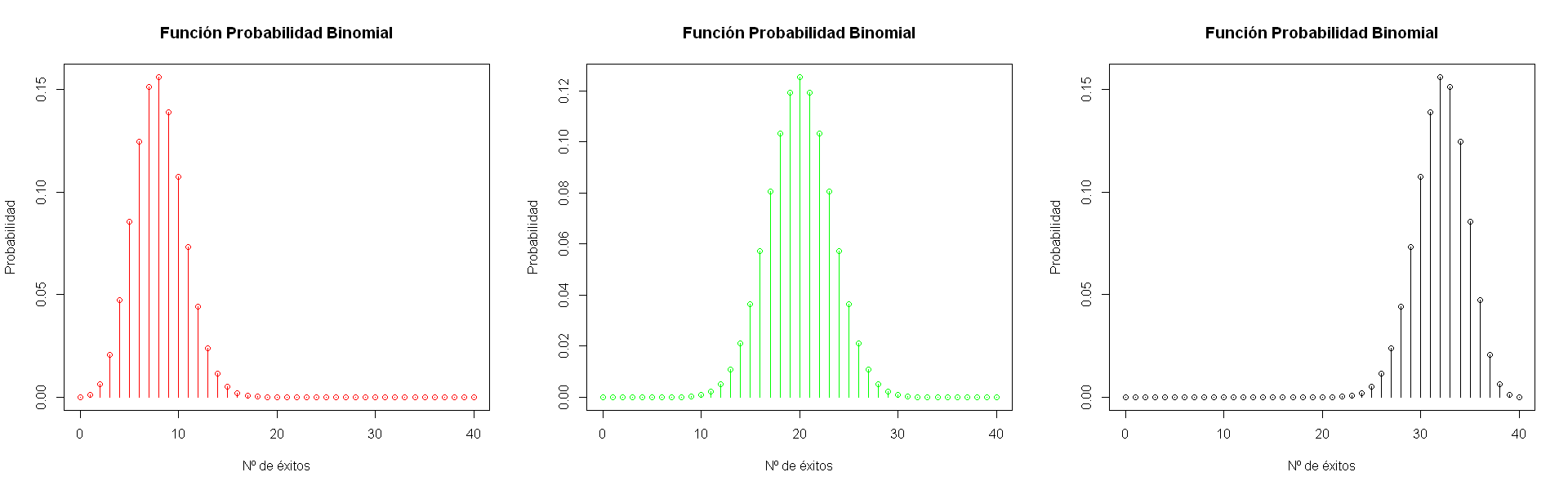
Suponga que se realizan \(N\) ensayos independientes idénticos Bernoulli de parámetro \(p\). La v.a. X que representa el número \(k\) de ensayos existosos entre los \(N\) ensayos realizados, se denomina Binomial y cumple:
\(\begin{array}{lll} P(X=k) & = & {N \choose k} p^k (1-p)^{N-k}, \qquad k=0,1,...N \\ E[X] & = & Np\\ Var(X) & = & Np(1-p)\\ Asimetria(X) & = & \frac{1-2p}{\sqrt{np(1-p)}}\\ Curtosis(X) & = & \frac{1-6p(1-p)}{np(1-p)}\\ \end{array}\)
options(repr.plot.width=16, repr.plot.height=5)
par(mfrow=c(1,3))
vec <- seq(0,40,by=1)
par(cex = 0.8)
pvec1 <- dbinom(vec,prob=0.2,size=40)
pvec2 <- dbinom(vec,prob=0.5,size=40)
pvec3 <- dbinom(vec,prob=0.8,size=40)
plot(vec,pvec1,type="h",col = "red", xlab = "Nº de éxitos", ylab = "Probabilidad", main = "Función Probabilidad Binomial")
points(vec,pvec1,col="red")
plot(vec,pvec2,type="h",col = "green", xlab = "Nº de éxitos", ylab = "Probabilidad", main = "Función Probabilidad Binomial")
points(vec,pvec2,col="green")
plot(vec,pvec3,type="h",col = "black", xlab = "Nº de éxitos", ylab = "Probabilidad", main = "Función Probabilidad Binomial")
points(vec,pvec3,col="black")
4.3. Distribución Exponencial¶
Sea \(X\) v.a. continua, es exponencial de tasa \(\lambda\) si su densidad de probabilidad cumple:
\(\begin{array}{lll} f_X(x) & = & \lambda exp(-\lambda x)\qquad, 0 \leq x <\infty\\ F_X(x) & = & 1- exp(-\lambda x)\\ E[X] &= &\frac{1}{\lambda}\\ Var(X)& =& \frac{1}{\lambda^2}\\ Asimetria(X) & = & 2\\ Curtosis(X) & = & 9 \\ \end{array}\)
##distribución exponencial
library("rbokeh")
vec <- seq(0,5,by=0.05)
pvec1 <- dexp(vec,2)
pvec2 <- dexp(vec,1)
pvec3 <- dexp(vec,0.5)
p <- figure(plot_width=600,plot_height=200, title="Densidad Exponencial", title_location="above", legend_location = "top_right") %>%
ly_lines(vec,pvec1,legend="l=2") %>%
ly_lines(vec,pvec2,col="blue",legend="l=1") %>%
ly_lines(vec,pvec3,col="red",legend="l=0.5")
p
4.4. Distribución Normal o Gaussiana¶
Sea \(X\) v.a. continua, es normal de media \(\mu\) y varianza \(\sigma^2\) y se denota \(\cal{N}(\mu,\sigma^2)\) si su densidad de probabilidad cumple:
\(\begin{array}{lll} f_X(x) & = & \frac{1}{\sqrt{2\pi}\sigma} exp(\frac{-(x-\mu)^2}{2\sigma^2})\qquad, -\infty < x <\infty\\ E[X] &= &\mu\\ Var(X)& =& \sigma^2\\ Asimetria(X) & = & 0\\ Curtosis(X) & = & 3 \\ \end{array}\)
Esta es la distribución de probabilidad mas utilizada. Muchas variables se distribuyen aproximadamente normales (altura, peso, satisfacción en el trabajo, etc.).
Permite modelar los errores o ruidos.
Teorema de límite central, tests de hipótesis paramétricos, inferencia estadística clásica.
¿Cómo se verifica que una v.a. sigue una distribución normal?
Test de normalidad de Shapiro-Wilk, Q-Q plot
##Distribución Gaussiana
vec <- seq(-6,6,by=0.05)
pvec1 <- dnorm(vec,0,0.4)
pvec2 <- dnorm(vec,0,1)
pvec3 <- dnorm(vec,0,3)
pvec4 <- dnorm(vec,-2,0.6)
p <- figure(plot_width=600,plot_height=200, title="Densidad Gaussiana", title_location="above", legend_location = "top_right") %>%
ly_lines(vec,pvec1,legend="m=0, s=0.4") %>%
ly_lines(vec,pvec2,col="blue",legend="m=0, s==1") %>%
ly_lines(vec,pvec3,col="red",legend="m=0, s=3") %>%
ly_lines(vec,pvec4,col="green",legend="m=-2, s=0.6")
p
4.4.1. Distribución Normal Estandarizada¶
\(Z \sim \cal{N}(0,1)\) si su densidad de probabilidad cumple:
\(\begin{array}{lll} f_X(x) & = & \frac{1}{\sqrt{2\pi}} exp(\frac{-x^2}{2})\qquad, -\infty < x <\infty\\ E[X] &= &0\\ Var(X)& =&1\\ \end{array}\)
Si \(X \sim \cal{N}(\mu,\sigma^2)\), entonces \(Z = \frac{X-\mu}{\sigma} \sim \cal{N}(0,1)\)
Esta transformación se denomina “Z-score” y se utiliza incluso si la v.a. no cumple el supuesto de normalidad. Se suele denominar estandarización o normalización.
Regla Empírica 68-95-99.7
Si \(X \sim \cal{N}(\mu,\sigma^2)\), entonces:
\(\begin{array}{lll} P(\mu-\sigma < X < \mu+\sigma) & = & 0.68\\ P(\mu-2\sigma < X < \mu+2\sigma) & = & 0.95\\ P(\mu-3\sigma < X < \mu+3\sigma) & = & 0.997\\ \end{array}\)
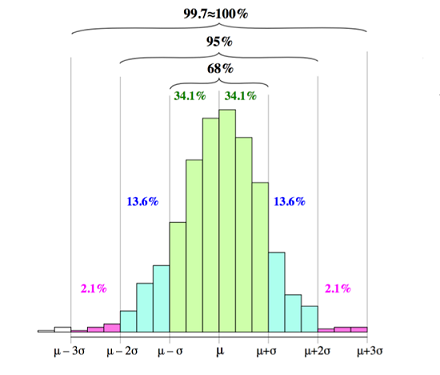
Muy útil para la detección de outliers, bajo el supuesto de normalidad.
