.ipynb .pdf

repositorio

Binder

Contenido

10. Inferencia en Estadística Paramétrica

• Distribuciones de estadísticos muestrales

• Intervalos de Confianza

• Test de Hipótesis

10.1. Distribuciones de estadísticos muestrales

Muestra o muestra aleatoria:

Sean \(X_1,\cdots,X_n\) v.a.i.i.d de distribución \(F\), entonces los valores que toman dichas variables \(\{x_1,\cdots,x_n\}\) representan una muestra aleatoria de la distribución \(F\).

Estadístico:

Es una variable aleatoria cuyo valor se puede determinar a partir de los datos muestrales:

\[Y = T(X_1,\cdots, X_n)\]

donde T es un operador sobre el espacio muestral \(X_1,\cdots,X_n\) que devuelve una v.a. a valores reales. Es decir

\[y = Y(\omega) = T(X_1(\omega),\cdots,X_n(\omega)) \in {\rm I\!R}\]

Ejemplos: media muestral, varianza muestral.

Distribución de muestreo:

La distribución de probabilidad de un estadístico dado.

10.1.1. Media muestral

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. de distribución \(F\) entonces se define la media muestral como:

\[\bar{X} = \frac{1}{n}{\displaystyle \sum_{i=1}^n} X_i\]

Propiedades

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \(\sim F\), \(\mu = E[X_i], \sigma^2 = Var[X_i]\) media y varianza teórica de \(F\). Entonces se cumple:

\[E(\bar{X})= E \left(\frac{1}{n}\sum_{i=1}^n X_i\right) = \frac{1}{n} \sum_{i=1}^n E[X_i] = \frac{1}{n} \sum_{i=1}^n \mu = \mu\]

con lo cual \(\bar{X}\) es un estimador insesgado de \(\mu\).

\[Var(\bar{X})= Var \left(\frac{1}{n}\sum_{i=1}^n X_i\right) = \frac{1}{n^2} \sum_{i=1}^n Var[X_i] = \frac{1}{n^2} \sum_{i=1}^n \sigma^2 = \frac{\sigma^2}{n}\]

10.1.2. Varianza muestral

Sean \(X_1,\cdots,X_n\) v.a.i.i.d de distribución \(F\) entonces se define la varianza muestral como:

\[S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 \]

La desviación estándar muestral se define como

\[S = \sqrt{ \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 }\]

Propiedades

\[ (n-1) S^2 = \sum_{i=1}^n(X_i - \bar{X})^2 = \sum_{i=1}^nX_i^2 - 2\bar{X}\sum_{i=1}^n X_i + n\bar{X}^2 = \sum_{i=1}^nX_i^2 - n\bar{X}^2 \]

Entonces:

\[E(S^2)= E \left[\frac{1}{n-1}\left(\sum_{i=1}^nX_i^2 - n\bar{X}^2\right)\right] = \frac{1}{n-1} \left(\sum_{i=1}^n E[(X_i^2)] - n E[\bar{X})^2]\right)\]

Dado que }

\[E[X_i^2] = \sigma^2 + \mu^2\qquad \text{y} \qquad E[\bar{X}^2]= \frac{\sigma^2}{n} + \mu^2\]

entonces

\[E(S^2)=\frac{1}{n-1}\left(n\sigma^2+n\mu^2 - n\frac{\sigma^2}{n} - n\mu^2\right) = \frac{n-1}{n-1}\sigma^2 = \sigma^2\]

De esta manera \(S^2\) es un estimador insesgado de \(\sigma^2\)

10.1.3. La distribución chi-cuadrado

Sean \(Z_1,\cdots, Z_k\, v.a.i.i.d. \, \sim {\it N}(0,1)\) entonces

\[ Y = Z_1^2+\cdots+Z_k^2 \sim \chi_{(k)}^2\]

donde \(k\) son los grados de libertad de la distribución.

La función de densidad de probabilidad de una chi-cuadrado cumple:

\(\begin{equation} \begin{array}{ll} f(x;k) = \left\{\begin{array}{ll} {\frac{1}{2^{k/2}\Gamma(k/2)}}x^{(k/2)-1}e^{-x/2} & x\, >0\\ 0 & x\, \leq0\\ \end{array} \right .\\ \end{array} \end{equation}\)

con

\[\Gamma(\alpha) = \int_0^{\infty} x^{\alpha-1} e^{-x}dx\]

Además

\(\begin{equation} E[X]= k \\ Var[X]= 2k \\ \end{equation}\)

suppressMessages(library(dplyr))
suppressMessages(library(plotly))
suppressMessages(library(ggplot2))
suppressMessages(library(rmarkdown))

vec <- seq(0,20,by=0.05)
params <- c(1,2,3,4,5,6,7,8,9,10)
pvec <- list()
for (i in 1:length(params)){
    pvec[[i]] <- dchisq(vec,df=params[i],ncp=0)
}

steps <- list()
fig <- plot_ly(width=600,height=600) %>% layout(title = "\n \n Densidad de Probabilidad Chi-cuadrado",
                                                 yaxis = list(range=c(0,0.5)))
for (i in 1:length(params)){
    
    fig <- add_lines(fig, x=vec, y=pvec[[i]], 
                     visible=if (i==1) TRUE else FALSE,
                     mode='lines', line=list(color='blue'), showlegend=FALSE)
    steps[[i]] = list(args = list('visible', rep(FALSE, length(params))), 
                      label=params[i], method='restyle')
    steps[[i]]$args[[2]][i] = TRUE
}
fig <- fig %>% layout(sliders = list(list(active=0, 
                                          currentvalue = list(prefix = "df: "),
                                          steps=steps)))

#embed_notebook(fig)

fig

Propiedad de suma de v.a. chi-cuadrado independientes

Sean \(X\) e \( Y\) dos v.a. independientes con \(X \sim \chi^2_{(n)}\) e \(Y \sim \chi^2_{(m)}\) entonces se cumple: \( X+Y \sim \chi^2_{(n+m)}\)

10.1.4. Distribución de la media y varianza muestral: Caso Normal

Teorema de Fisher-Cochran

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu,\sigma^2)\) entonces la media y varianza muestral cumplen:

\(\begin{equation} \begin{array}{lcll} (i) & \bar{X} &\sim& {\cal N}(\mu, \frac{\sigma^2}{n})\\ (ii) & {\displaystyle \frac{(n-1)S^2}{\sigma^2}}& \sim& \chi_{(n-1)}^2 \\ (iii)& \bar{X} &{\mathrel \perp} & S^2\\ \end{array} \end{equation}\)

Para la demostración de este teorema se sugiere lo siguiente:

i) Utilice el Teo Fundamental Distribuciones Normales: la combinación lineal de v.a. independientes Normales es Normal (usa funciones generatrices de momentos)

(ii)y (iii) Se muestra primero para \(Y_i=\frac{X_i-\mu}{\sigma} \sim {\cal N}(0,1)\).

En efecto si se cumple para \(Y_i, i=1,\cdots,n\), se cumple para \(X_i, i=1,\cdots,n\) puesto que:

\[\bar{Y} = \frac{\bar{X} - \mu}{\sigma} \qquad \text{y}\qquad (n-1)S_Y^2 = \frac{(n-1) S_X^2}{\sigma^2}\]

Para ello se considera una transformación ortogonal \(A\) tal que \((Z_1,\cdots,Z_n) = AY^T\) conserva la independencia entre \(Z_i \sim {\cal N}(0,1)\) de manera que \(\bar{Y}\) es función lineal de \(Z_1\) y \(S^2\) de \(Z_2^2,\cdots Z_n^2\).

10.1.5. La distribución t-student

Sean \(Z \sim {\it N}(0,1)\) y \(X \sim \chi^2_{(n)}\), se define la v.a.

\[T = \frac{Z}{\sqrt{\frac{X}{n}}} \sim {\cal t}_{(n)}\]

que sigue una distribución t-student de n grados de libertad

Su función de densidad de probabilidad es:

\[ f(x) = f(t) = \frac{\Gamma(\frac{n+1}{2})} {\sqrt{n\pi}\,\Gamma(\frac{n}{2})} \left(1+\frac{t^2}{n} \right)^{\!-\frac{n+1}{2}},\! \]

y la media y varianza:

\(\begin{equation} \begin{array}{lll} E[X] &= &0\\ Var(X)& =& \dfrac{n}{n-2}\\ \end{array} \end{equation}\)

La varianza esta definida para valores de \(n \gt 2\).

Grados de Libertad (df)

Los grados de libertad se refieren al número de valores que pueden variar libremente, dado un conjunto de restricciones matemáticas (o número de parámetros estimados), en una muestra que se utiliza para estimar las características de una población.

Por ejemplo, para estimar la varianza de una población, primero se estidma la media de la población. Por lo tanto, si estimamos la varianza de la población con n observaciones, esta estimación tiene (n-1) grados de libertad. Asi, en un t-test de una muestra, un grado de libertad se utiliza en estimar la media y los n-1 restantes en estimar la variabilidad.

vec <- seq(-5,5,by=0.05)
params <- seq(1,20,by=1)
pvec <- list()
for (i in 1:length(params)){
    pvec[[i]] <- dt(vec,df=params[i])
}

steps <- list()
fig <- plot_ly(width=600,height=600) %>% layout(title = "\n \n Densidad de Probabilidad t-sudent",   yaxis = list(
      range=c(0,0.45)))
for (i in 1:length(params)){
    
    fig <- add_lines(fig, x=vec, y=pvec[[i]], 
                     visible=if (i==1) TRUE else FALSE,
                     mode='lines', line=list(color='red'), showlegend=FALSE)
    steps[[i]] = list(args = list('visible', rep(FALSE, length(params))), 
                      label=params[i], method='restyle')
    steps[[i]]$args[[2]][i] = TRUE
}
fig <- fig %>% layout(sliders = list(list(active=0, 
                                          currentvalue = list(prefix = "df: "),
                                          steps=steps)))

#embed_notebook(fig)

fig

Percentiles de t-student Sea \(t_{\alpha,n}\) tal que \(P(T_{(n)} \geq t_{\alpha,n}) = \alpha\) el percentil \((1-\alpha)\) de \(T_{(n)}\).

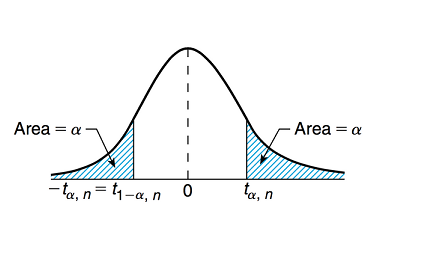
y \(t_{\frac{\alpha}{2},n-1}\) tal que \(P(T_{(n-1)} \geq t_{\frac{\alpha}{2},n-1}) = \frac{\alpha}{2}\) el percentil \((1-\frac{\alpha}{2})\) de \(T_{(n-1)}\).

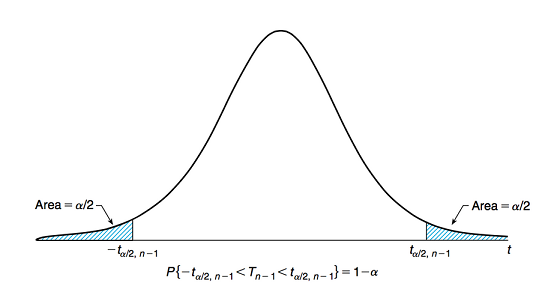
Corolario ( del Teo Fisher-Cochran)

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\it N}(\mu,\sigma^2)\) entonces se cumple:

\[ \sqrt{n} \frac{(\bar{X} - \mu)}{S} \sim t_{(n-1)}\]

10.1.6. Teorema del Límite Central

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. según una distribución de probabilidad \(F\) con media \(\mu\) y varianza \(\sigma^2\), entonces las media muestral \(\bar{X}\) cumple:

\[ \lim_{n \to \infty}P\left( \frac{\bar{X}- \mu}{\frac{\sigma}{\sqrt{n}}} \leq z\right) = F_Z(z) \qquad Z \sim \cal{N}(0,1)\]

se dice que

\[ \frac{(\bar{X} - \mu)}{\frac{\sigma}{\sqrt{n}}} \xrightarrow[n\rightarrow{}\infty]{\;\; \cal{D} \;\; } {\cal N}(0,1)\]

Es decir que la media muestral se aproxima a una distribución Normal de media \(\mu\) y varianza \(\frac{\sigma^2}{n}\) cuando \(n\) es grande. \(F\) es cualquier distribución de probabilidad, continua o discreta.

10.1.7. Ilustración

Simulando 100 muestras de distintos tamaños de una distribución definida, y elaborando histogramas de las medias muestrales se obtiene lo siguiente:

#caso binomial
params <- seq(5,100,by=5)
np <- 
muestra <- matrix(0,nrow=100,ncol=length(params))
for (i in 1:length(params)){
   
    n= params[i]
    size= n*100
    m <- matrix(rbinom(size,5,0.4),nrow=100,ncol=n,byrow=TRUE)
    medias <- m%*%rep(1,n)/n
    
    muestra[,i] <- (medias-2)/sqrt(0.6*0.4)
}

vec <- seq(-4,4,by=0.05)

steps <- list()
fig <- plot_ly(width=600,height=600) %>% layout(title = "\n \n Histograma de medias muestrales, caso binomial",   yaxis = list(
      range=c(0,0.4)), xaxis = list(range=c(-4,4)))

for (i in 1:length(params)){
    
    fig <- add_histogram(fig, muestra[,i],histnorm = "probability",showlegend=FALSE) 
  
    steps[[i]] = list(args = list('visible', rep(FALSE, length(params))), 
                      label=params[i], method='restyle')
    steps[[i]]$args[[2]][i] = TRUE
}
fig <- fig %>% layout(sliders = list(list(active=0, 
                                          currentvalue = list(prefix = "N: "),
                                          steps=steps)))

#embed_notebook(fig)

fig

10.1.8. ¿Cómo definir n suficientemente grande?

Depende de la distribución poblacional de los datos muestrales. Si la población es normal, la media muestral de distribuye normal independientemente del tamaño.

Regla consensuada: muestra aleatoria de tamaño muestral \(n \geq 30\).

10.2. Estimación de Intervalos de confianza

Objetivo

Obtener un intervalo con una cierta confianza de que el parámetro poblacional se encuentra ahí. Transitar de la estimación puntual al intervalo de confianza, nos permite ganar en precisión de la estimación al mismo tiempo que incorporamos un cierto nivel de confianza.

10.2.1. Definición

Un intervalo de confianza \((1-\alpha)\) para un parámetro \(\theta\) es un intervalo \(C_n = (a,b)\)

\[\mbox{ con } a= a(X_1,\cdots,X_n) \qquad\mbox{ y } \qquad b= b(X_1,\cdots,X_n) \]

funciones de los datos tales que:

\[P_{\theta}(\theta \in C_n) \geq 1-\alpha \qquad \forall \theta \in \Theta\]

donde \((1-\alpha)\) es la cobertura del intervalo de confianza

Ejemplo

Suponga que el tiempo de llegada al trabajo de las personas que viven en Valdivia sigue una distribución Normal de media \(\mu\) y varianaza \(\sigma^2\). Considere que se tiene una muestra aleatoria de 45 personas que trabajan en Valdiva, cuyo tiempo promedio de llegada al trabajo es de 21 minutos con desviación estandar muestral de 9 minutos.

Al calcular un intervalo de confianza al 95% (mas adelante aprenderemos como hacerlo) para la media de la muestra, usando la distribución t-student, se obtiene \((18.3, 23.7)\).

Interpretaciones erróneas de los Intervalos de Confianza

(i)Al \(95\%\) de los 45 trabajadores les toma entre 18.3 y 23.7 minutos llegar al trabajo.

Falso. El intervalo de confianza concierne a todos los trabajadores, no sólo a los 45 de la muestra.

(ii) Hay un \(95\%\) de posibilidades de que el tiempo medio que les tome llegar a su trabajo a todos lo trabajadores de Valdivia, esté entre 18.3 y 23.7 minutos.

Falso. Asi descrita, parece una afirmación sobre las probabilidades de las v.a. que definen los extremos del intervalo.

Interpretaciones correctas de los Intervalos de Confianza

(i)Tenemos una confianza del \(95\%\) de que el tiempo medio que les toma llegar a su trabajo a todos lo trabajadores de Valdivia, está entre 18.3 y 23.7 minutos, o bien que la media teórica de la distribución se encuentra entre 18.3 y 23.7 minutos.

(ii)Si se extrajeran múltiples muestras aleatorias de la misma población y se calcularan los intervalos de confianza al \(95\%\) para cada muestra, esperamos que la media de la población se encuentre en el \(95\%\) de esos intervalos, o que el \(95\%\) de los intervalos contenga la media teórica.

10.2.2. ¿Cómo calcular un Intervalo de Confianza?

Clave

Obtener la distribucioón de probabilidad del estimador puntual

Foco en esta sesión:

Poblaciones distribuidas normalmente para estimar intervalos de confianza de la media o la diferencia de medias.

10.2.3. Caso 1: Media de distribución Normal con varianza conocida

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu,\sigma^2)\) entonces, por el Teo de Fisher-Cochran se cumple

\[ Z = \frac{ \bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim {\cal N}(0,1)\]

Sea \(z_{\frac{\alpha}{2}}\) tal que

\[P(-z_{\frac{\alpha}{2}}\leq Z \leq z_{\frac{\alpha}{2}}) = 1-\alpha\]

Entonces se define el intervalo de confianza del \(100(1-\alpha)\%\) para \(\mu\) como:

\[\left(\bar{x} - z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}, \bar{x} + z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\right )\]

Ejemplo: Suponga que cuando una señal de valor \(\mu\) es transmitida desde una ubicación A, el valor que se recibe en la localización B sigue una distribución normal de media \(\mu\) y varianza \(2\). Considere que para reducir el error, se ha enviado nueve veces el mismo valor. Los sucesivos valores recibidos son: \(5, 8.5, 12, 15, 7, 9, 7.5, 6.5, 10.5\). Construya un intervalo de confianza al \(95\%\) para \(\mu\).

Vemos que \(\bar{x} = \frac{81}{9} = 9\), por otra parte resulta que para \(100(1-\alpha)\% = 95\%\) se tiene que \(z_{\frac{\alpha}{2}}= z_{0.025} = 1.96\)

datos <- c(5, 8.5, 12, 15, 7, 9, 7.5, 6.5, 10.5)
media <- mean(datos)
sigma <- sqrt(2)
n <- 9
rango1 <- media - 1.96*sigma/sqrt(n)
rango2 <- media + 1.96*sigma/sqrt(n)
print(c(media, sigma,rango1, rango2))

[1] 9.000000 1.414214 8.076047 9.923953

10.2.4. Caso 2: Media de distribución Normal con varianza desconocida

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\it N}(\mu,\sigma^2)\) entonces, del Corolario del Teo de Fisher-Cochran se cumple:

\[ \frac{(\bar{X} - \mu)}{\frac{S}{\sqrt{n}}} \sim t_{(n-1)}\]

Sea \(t_{(n-1),\frac{\alpha}{2}}\) tal que

\[P(-t_{(n-1),\frac{\alpha}{2}}\leq t_{(n-1)} \leq t_{(n-1),\frac{\alpha}{2}}) = 1-\alpha\]

Entonces se define el intervalo de confianza del \(100(1-\alpha)\%\) para \(\mu\) como:

\[\left(\bar{x} - t_{(n-1),\frac{\alpha}{2}}\frac{S}{\sqrt{n}}, \bar{x} + t_{(n-1),\frac{\alpha}{2}}\frac{S}{\sqrt{n}}\right )\]

datos <- c(5, 8.5, 12, 15, 7, 9, 7.5, 6.5, 10.5)
media <- mean(datos)
s <- sd(datos)
n <- 9
rango1 <- media - 2.306*s/sqrt(n)
rango2 <- media + 2.306*s/sqrt(n)
print(c(media, s,rango1, rango2))

[1]  9.000000  3.082207  6.630810 11.369190

El supuesto de normalidad Notar que los intervalos de confianza para media muestral aquí construidos, se pueden generalizar para el caso de muestras aleatorias que provienen de otras distribuciones de probabilidad distintas a la normal.

En efecto, del Teo del Límite Central se tiene que para \(n\) suficientemente grande (\(n \geq 30\), si la distribucion no es muy asimétrica) :

\[ \frac{(\bar{X} - \mu)}{\frac{\sigma}{\sqrt{n}}} \approx {\cal N}(0,1)\]

y mas aún, del Teorema de Slutsky se tiene:

\[ \frac{(\bar{X} - \mu)}{\frac{S}{\sqrt{n}}} \approx {\cal N}(0,1)\]

10.2.5. Caso 3: Diferencia de Medias de dos distribuciones Normales con varianzas conocidas

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu_1,\sigma_1^2)\) y \(Y_1,\cdots,Y_m\) v.a.i.i.d. \({\cal N}(\mu_2,\sigma_2^2)\) Suponga además que ambas muestras aleatorias son independientes. En lo que sigue construiremos un intervalo de confianza para la diferencia de medias \(\mu_1-\mu_2\)

del Teo de Fisher-Cochran se cumple:

\[ \bar{X} \sim {\cal N}(\mu_1,\frac{\sigma_1^2}{n})\]

\[ \bar{Y} \sim {\cal N}(\mu_2,\frac{\sigma_2^2}{m})\]

Como \(\bar{X}\) es independiente de \(\bar{Y}\), ambas distribuidas normales, entonces

\[ \bar{X}- \bar{Y} \sim {\cal N}(\mu_1 - \mu_2,\frac{\sigma_1^2}{n}+\frac{\sigma_2^2}{m})\]

Asi

\[Z = \frac{\bar{X}- \bar{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n}+\frac{\sigma_2^2}{m}}} \sim {\cal N}(0,1)\]

Sea \(z_{\frac{\alpha}{2}}\) tal que

\[P(-z_{\frac{\alpha}{2}}\leq Z \leq z_{\frac{\alpha}{2}}) = 1-\alpha\]

Entonces se define el intervalo de confianza del \(100(1-\alpha)\%\) para \(\mu_1 - \mu_2\) como:

\[\left(\bar{x}-\bar{y} - z_{\frac{\alpha}{2}}{\sqrt{\frac{\sigma_1^2}{n}+\frac{\sigma_2^2}{m}}}, \bar{x}-\bar{y} + z_{\frac{\alpha}{2}}{\sqrt{\frac{\sigma_1^2}{n}+\frac{\sigma_2^2}{m}}}\right )\]

10.3. Test de Hipótesis

En este caso se trata de utilizar una muestra aleatoria de la población para probar una hipótesis particular sobre los parámetros (en lugar de estimar explícitamente parámetros desconocidos de una distribución poblacional).

10.3.1. ¿Qué es una hipótesis estadística?

Es una afirmación acerca de un parámetro poblacional.

La hipótesis nula \(H_0\) y la alternativa \(H_1\) son mutuamente exclusivas, pueden o no ser complementarias, de uno o dos lados.

Ejemplo:

\[H_0: \mu = \mu_0\]

\[H_1: \mu \neq \mu_0\]

Un test de hipótesis es una regla que especifica: para que valores muestrales no se rechaza la hipótesis nula \(H_0\), y para que valores muestrales se rechaza la hipótesis nula \(H_0\) en favor de \(H_1\). El subconjunto \(C\) del espacio muestral en donde se rechaza la hipótesis nula se denomina “región de rechazo” o “región crítica”, y su complemento la “región de aceptación”.

Se trata de desarrollar un procedimiento para determinar si una muestra de datos es consistente con la hipotésis nula o no. Para ello se utiliza un estadístico (una función de la muestra) y se observa un valor de este estadístico.

10.3.2. Tipos de Errores y nivel de significancia

• \(\alpha\) se denomina nivel de significancia del test

• \((1-\beta)\) se denomina potencia del test

Ambos errores deben ser considerados. Comenzaremos por manejar el error de tipo I.

10.3.3. Caso 1: Test Media de Dist. Normal con varianza conocida: enfoque del valor crítico.

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu,\sigma^2)\) con media desconocida \(\mu\) y varianza conocida \(\sigma^2\), y consideremos el test:

\[H_0: \mu = \mu_0\]

\[H_1: \mu \neq \mu_0\]

con \(\mu_0\) un valor específico dado.

• utilizaremos la media muestral \(\bar{x}\) como una estimación puntual natural de \(\mu\)

• rechazaremos \(H_0\) si \(\bar{x}\) está suficientemente lejos de \(\mu_0\) y no la rechazamos en caso contrario.

• ¿qué es suficientemente lejos? Se define la región de rechazo

\[C = \{X_1,\cdots X_n : |\bar{X} - \mu_0 | \geq c\}\]

• queremos controlar el error de tipo I, \(\alpha\):

\[P_{H_0}( |\bar{X} - \mu_0 | \geq c) = \alpha\]

Como bajo \(H_0\) se cumple:

\[ Z = \frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \sim {\cal N}(0,1)\]

Sea \(z_{\frac{\alpha}{2}}\) tal que

\[P(|Z| \geq z_{\frac{\alpha}{2}}) = \alpha\]

entonces

\[P\left(\left|\frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\right| \geq z_{\frac{\alpha}{2}}\right) = \alpha\]

de manera que se rechaza \(H_0\) si

\[\left|\frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\right| \geq z_{\frac{\alpha}{2}}\]

Y NO se rechaza \(H_0\) si

\[\left|\frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\right| \leq z_{\frac{\alpha}{2}}\]

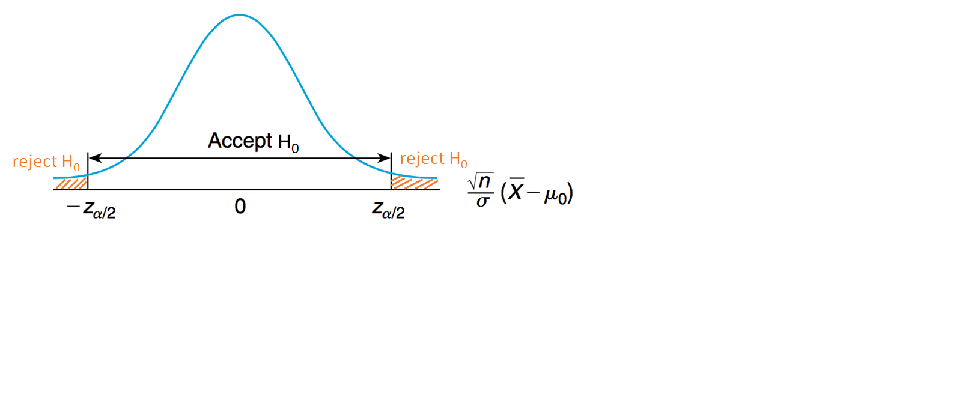
10.3.4. Caso 2: Test de Media de Dist. Normal con varianza conocida: enfoque del p-value

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu,\sigma^2)\) con media desconocida \(\mu\) y varianza conocida \(\sigma^2\), y consideremos el test:

\[H_0: \mu = \mu_0\]

\[H_1: \mu \neq \mu_0\]

con \(\mu_0\) un valor específico dado.

El p-value es la probabilidad de observar un valor del estadístico del test igual o mas extremo que el observado, asumiendo que \(H_0\) es verdadero. Es la menor significancia con la cual podemos rechazar \(H_0\).

• utilizaremos la media muestral \(\bar{x}\) como una estimación puntual natural de \(\mu\)

• especificamos un valor para la significancia \(\alpha\)

• calculamos el estadístico

\[ z = \frac{ \bar{x}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\]

• y el p-value

\[p = 2 P(Z \geq |z|)\]

Si \(p \leq \alpha\) se rechaza \(H_0\)

Si \(p \gt \alpha\) NO se rechaza \(H_0\)

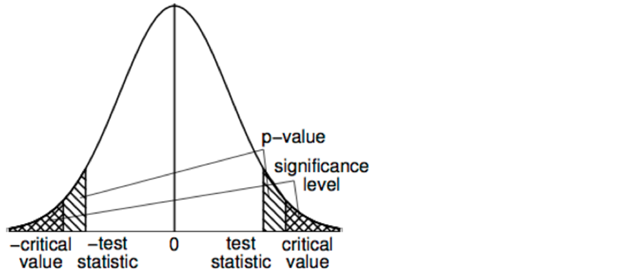
El p-value es una medida de evidencia para rechazar \(H_0\): cuanto menor el p-value, mayor es la evidencia para rechazar \(H_0\).

Error conceptual común: el p-value no es la probabilidad de que la hipótesis nula sea verdadera, no es \(P(H_0\)) ni \(P(H_0 \mid data)\).

Relación entre p-value y regiones críticas para el caso ya estudiado

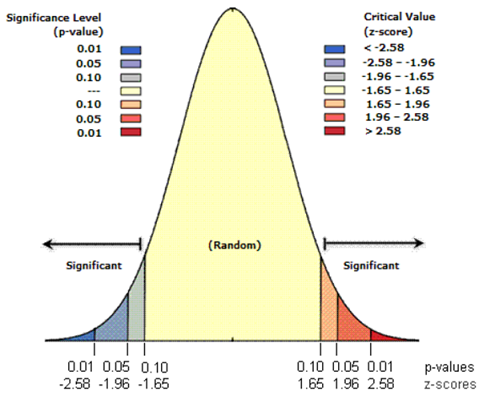
z = (8.5-8)/sqrt(2/5)
p_value = 2*(1-pnorm(z))
print(c(z, p_value))

[1] 0.7905694 0.4291953

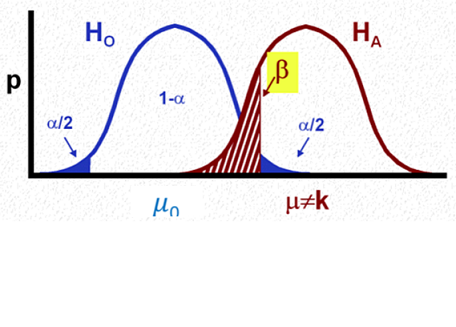
Y el error de tipo II?

Como medimos el error de no rechazar \(H_0\) cuando \(H_1\) es verdadero?

La difultad que encontramos es que la especificación de \(H_1\) es bastante amplia:

\[H_1 : \mu \neq \mu_0\]

Asumiremos que la media poblacional es \(\mu \neq \mu_0\).

Para el caso que hemos estado estudiando: población normal con varianza conocida, podemos hacer la siguiente derivación:

\(\begin{array}{lll} \beta(\mu) & = & P_{\mu}\{no\, rechazar\, H_0\}\\ &&\\ & = & P_{\mu}\left\{\left|\frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\right| \leq z_{\frac{\alpha}{2}}\right \}\\ &&\\ & = & P_{\mu}\left\{ -z_{\frac{\alpha}{2}} \leq \frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\leq z_{\frac{\alpha}{2}}\right \}\\ &&\\ & = & P_{\mu}\left\{ -z_{\frac{\alpha}{2}}-\frac{\mu}{\frac{\sigma}{\sqrt{n}}} \leq \frac{ \bar{X}-\mu_0 - \mu}{\frac{\sigma}{\sqrt{n}}}\leq z_{\frac{\alpha}{2}} -\frac{\mu}{\frac{\sigma}{\sqrt{n}}}\right \}\\ &&\\ & = & P_{\mu}\left\{ -z_{\frac{\alpha}{2}}-\frac{\mu}{\frac{\sigma}{\sqrt{n}}} \leq Z - \frac{\mu_0}{\frac{\sigma}{\sqrt{n}}} \leq z_{\frac{\alpha}{2}} -\frac{\mu}{\frac{\sigma}{\sqrt{n}}}\right \}\\ &&\\ & = & P_{\mu}\left\{ \frac{\mu_0 -\mu}{\frac{\sigma}{\sqrt{n}}}-z_{\frac{\alpha}{2}} \leq Z \leq \frac{\mu_0 - \mu}{\frac{\sigma}{\sqrt{n}}}+ z_{\frac{\alpha}{2}} \right \}\\ &&\\ & = & \Phi\left (\frac{\mu_0 -\mu}{\frac{\sigma}{\sqrt{n}}}+z_{\frac{\alpha}{2}}\right) - \Phi\left (\frac{\mu_0 -\mu}{\frac{\sigma}{\sqrt{n}}}-z_{\frac{\alpha}{2}}\right) \end{array}\)

mu0=0
sigma0=6
n=10
alpha= 0.05
perc_i= qnorm(alpha/2,mean=mu0,sd=sigma0/sqrt(n))
perc_d = qnorm(1-alpha/2, mean=mu0,sd=sigma0/sqrt(n))
vec <- seq(-10+mu0,20+mu0,by=0.05)
a <- perc_i
b <- perc_d
vec2 <- seq(perc_i+0.05,perc_d-0.05,by=0.05)
vec_i <-  seq(-10+mu0+0.05,perc_i-0.05,by=0.05)
a_i = -10+mu0
b_i = perc_i
vec_d <- seq(perc_d+0.05,mu0+10-0.05,by=0.05)
a_d = perc_d
b_d = mu0+10
pvec0 <- dnorm(vec,mean=mu0,sd=sigma0/sqrt(n))
params <- c(1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10)
aval <- list()

for (i in 1:length(params)){
  aval[[i]] <-list(visible = FALSE,
                      y=dnorm(vec,mean=params[i],sd=sigma0/sqrt(n)))
                      
}

steps <- list()
fig <- plot_ly(width=600,height=400) %>% layout(title = "\n \n Error de tipo II en función de valor de la media",
                                                 yaxis = list(range=c(0,0.3))) %>%
        add_lines(x=vec,y=pvec0,line=list(color='red'),showlegend = FALSE) %>%
        add_polygons(x = c(a_i,vec_i,b_i), y =c(0,dnorm(vec_i,mean=mu0,sd=sigma0/sqrt(n)),0),fill='tozeroy',
                      fillcolor = 'rgba(255, 212, 96, 0.5)',line=list(color='rgba(255, 212, 96, 0.5)'),showlegend = FALSE)%>%
        add_polygons(x = c(a_d,vec_d,b_d), y =c(0,dnorm(vec_d,mean=mu0,sd=sigma0/sqrt(n)),0),fill='tozeroy',
                      fillcolor = 'rgba(255, 212, 96, 0.5)',line=list(color='rgba(255, 212, 96, 0.5)'),showlegend = FALSE)

for (i in 1:10){
    
   fig <- add_lines(fig,x=vec,  y=aval[[2*i]]$y, visible = aval[[2*i]]$visible,
                    type = 'scatter', mode = 'lines', line=list(color='blue'), showlegend = FALSE)
    
   fig <- add_polygons(fig,x = c(a,vec2,b), y =c(0,dnorm(vec2,mean=params[[2*i]],sd=sigma0/sqrt(n)),0),visible = aval[[2*i]]$visible,fill='tozeroy',
                       fillcolor = 'rgba(168, 216, 234, 0.5)',line=list(color='rgba(168, 216, 234, 0.5)'),showlegend = FALSE)
   
  step <- list(args = list('visible', rep(FALSE, 2*length(aval)+3)),
               method = 'restyle',label=i)
  step$args[[2]][2*i+2] = TRUE
  step$args[[2]][2*i+3] = TRUE  
  step$args[[2]][1] = TRUE
  step$args[[2]][2] = TRUE
  step$args[[2]][3] = TRUE
  steps[[i]] = step 
  
}  
length(steps)


# add slider control to plot
fig <- fig %>%
  layout(sliders = list(list(active = 0,
                             currentvalue = list(prefix = "mu_1: "),
                             steps = steps)))

#mbed_notebook(fig)

10

fig

10.3.5. Potencia

• \(\beta(\mu)\) se denomina curva característica operacional (OC) y representa la probabilidad de error de tipo II

• \(1 - \beta(\mu)\) se denomina función potencia o potencia estadística

• Para el caso aqui desarrollado, y para un nivel de significancia fija \(\alpha\), la curva OC es simétrica en torno a \(\mu_0\) y depende de \(\mu\) a través de \(d= \frac{\mu_0 -\mu}{\frac{\sigma}{\sqrt{n}}}\).

• el error de tipo II depende de el tamaño de la muestra \(n\), la varianza conocida \(\sigma^2\), el nivel de significancia \(\alpha\) y el tipo de test (de uno o dos lados) y la diferencia ente \(\mu\) y \(\mu_0\)

mu0=0
sigma0=6.0
alpha= 0.05
perc= qnorm(1-alpha/2)
perc
vec <- seq(mu0,20+mu0,by=0.05)

params <- seq(1,30,by=1)
aval <- list()

for (i in 1:length(params)){
  x_d = sqrt(params[i])*(mu0-vec)/sigma0 + perc
  x_i = sqrt(params[i])*(mu0-vec)/sigma0 - perc
             
  aval[[i]] <-list(visible = FALSE,
                      y=pnorm(x_d)-pnorm(x_i))
                      
}

1.95996398454005

steps <- list()
fig1 <- plot_ly(width=600,height=400) %>% layout(title = "\n \n Error de tipo II en función del tamaño de la muestra",
                                                yaxis = list(title = 'Beta'), xaxis = list(title = 'mu_1'))
for (i in 1:length(params)){
    
   fig1 <- add_lines(fig1, x=vec,  y=aval[[i]]$y, visible = aval[[i]]$visible,
                    type = 'scatter', mode = 'lines', line=list(color='blue'), showlegend=FALSE)
    
   
  step <- list(args = list('visible', rep(FALSE,length(aval))), method = 'restyle',label=params[i])
  step$args[[2]][i] = TRUE
  steps[[i]] = step 
  
}  
fig1 <- fig1 %>% layout(sliders = list(list(active=1, 
                                          currentvalue = list(prefix = "n: "),
                                          steps=steps)))
#embed_notebook(fig1)

fig1

¿Cómo incrementar la potencia estadística?

• aumentar el tamaño de la muestra

• disminuir la varianza

• aumentar la sgnificancia, manteniendo un equilibrio entre los errores de tipo I y II

• usar un test de un lado

¿En qué casos usar una test de un lado?

• si sabemos que los valores no pueden ser mayores (o menores) que \(\mu_0\)

• que interesa solamente el efecto en una dirección. Ejemplo, probar que un nuevo medicamento es mas efectivo que uno existente, dado que es mas barato.

Veamos el caso en que la hipótesis alternativa indica que el valor de la media es mayor que \(\mu_0\):

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu,\sigma^2)\) con media desconocida \(\mu\) y varianza conocida \(\sigma^2\), y consideremos el test:

\[H_0: \mu = \mu_0\]

\[H_1: \mu > \mu_0\]

con \(\mu_0\) un valor específico dado.

Entonces tenemos como antes que bajo \(H_0\):

\[ Z = \frac{ \bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \sim {\cal N}(0,1)\]

pero el test contrasta sólo respecto de valores a la derecha de la distribución, es decir:

\[P_{H_0}( Z <= z_{\alpha}) = 1- \alpha\]

De manera que:

• Se rechaza \(H_0\) si \( z > z_{\alpha}\)

• No se rechaza \(H_0\) en caso contrario

Desde el enfoque del p-value:

\[p = P_{H_0}( Z > z)\]

• Si \(p \leq \alpha\) se rechaza \(H_0\)

• Si \(p \gt \alpha\) NO se rechaza \(H_0\)

10.3.6. Caso 3: Test de Media de Dist. Normal con varianza desconocida

Sean \(X_1,\cdots,X_n\) v.a.i.i.d. \({\cal N}(\mu,\sigma^2)\) con media y varianzas desconocidas \((\mu, \sigma)\), y consideremos el test:

\[H_0: \mu = \mu_0\]

\[H_1: \mu \neq \mu_0\]

con \(\mu_0\) un valor específico dado.

En este caso tenmos que

\[ t = \frac{\bar{x}-\mu_0}{\frac{s}{\sqrt{n}}} \sim t_{n-1}\]

con

\[ s^2= \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2\]

Así el estadístico asociado al test es:

\[T_{n-1} = \left| \frac{ \bar{X}-\mu_0}{\frac{S}{\sqrt{n}}} \right |\]

y

\[P_{H_0}( |T_{n-1}| <= t_{\frac{\alpha}{2},n}) = 1- \alpha\]

De manera que:

• Se rechaza \(H_0\) si \(|T_{n-1}| > t_{\frac{\alpha}{2},n}\)

• No se rechaza \(H_0\) en caso contrario

Desde el enfoque del p-value:

\[p = 2 P_{H_0}( T_{n-1} > |t|)\]

• Si \(p \leq \alpha\) se rechaza \(H_0\)

• Si \(p \gt \alpha\) NO se rechaza \(H_0\)

10.3.7. Robustez

• Los estadísticos de test requieren provenir de una muestra aleatoria normal o una distribución t.

• Los test que dependen de \(Z\) son robustos respecto de la hipótesis de normalidad siempre que un tamaño de muestra suficientemente grande.

• Los test que depende de \(t\) son robustos respecto de la hipótesis de normalidad, en el sentido que la normalidad no tiene gran influencia en las tasas de error de tipo I

• Cuando la hipótesis de normalidad está muy lejos de cumplirse, se sugiere transformar los datos o usar test no-paramétricos como por ejemplo el test de Mann-Whitney.

anterior

9. Modelamiento parámetrico Bayesiano

siguiente

11. Inferencia estadística con tests no-paramétricos