12. Bootstrap no paramétrico¶

Bootstrap es una familia de técnicas de remuestreo que permiten obtener distribuciones muestrales para estimadores estadísticos. Las distribuciones muestrales pueden utilizarse para calcular intervalos de confianza o realizar tests de hipótesis. En este sentido bootstrap es una alternativa a los métodos tradicionales para hacer test de hipótesis basados en derivaciones algebraicas.

En esta lección estudiaremos el algoritmo de bootstrap original propuesto por Bradly Efron en 1979. Este algoritmo se basa en la técnica de muestreo con reemplazo.

Las principales ventajas de bootstrap son que

no requiere hacer supuestos sobre la distribución de la población
puede aplicarse para prácticamente cualquier estadístico muestral

La desventaja es que es relativamente más costoso (computacionalmente), sin embargo esta desventaja es cada vez menos relevante con la alta disponibilidad de capacidad de cómputo

12.1. Muestreo con reemplazo¶

El siguiente diagrama ejemplifica como opera el muestreo con reemplazo:

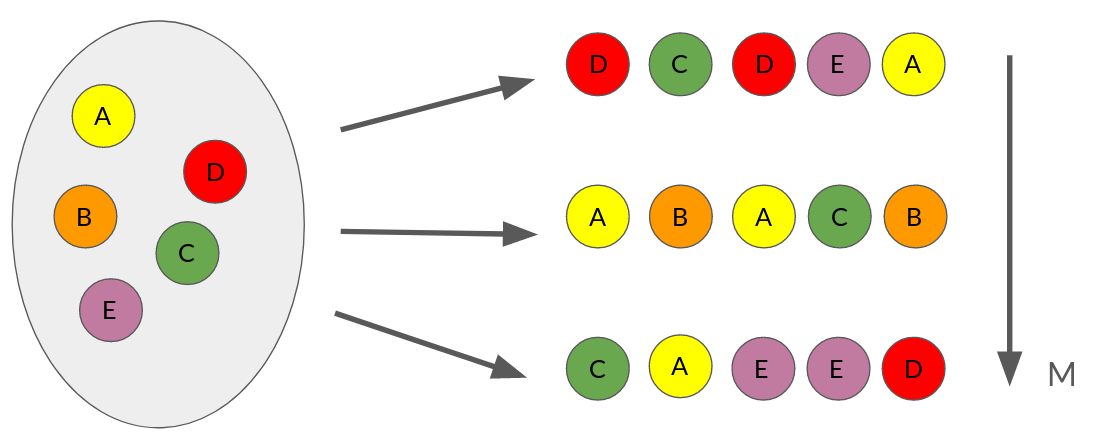
Para un dataset con \(N\) muestras se generan \(M\) copias del dataset todas de tamaño \(N\). En las copias algunas de las observaciones originales no aparecen mientras que otras pueden aparecer más de una vez, es decir que se remuestrea pero con reemplazo.

El objetivo de este procedimiento es simular el proceso que generó la muestra original a partir de la población. El muestreo con reeplazo hace que los datasets generados mantengan las propiedades del dataset original. El único supuesto para que esto se cumpla es que las muestras deben ser i.i.d.

12.2. Algoritmo de bootstrap¶

El siguiente esquema muestra el procedimiento general para obtener una distribución bootstrap

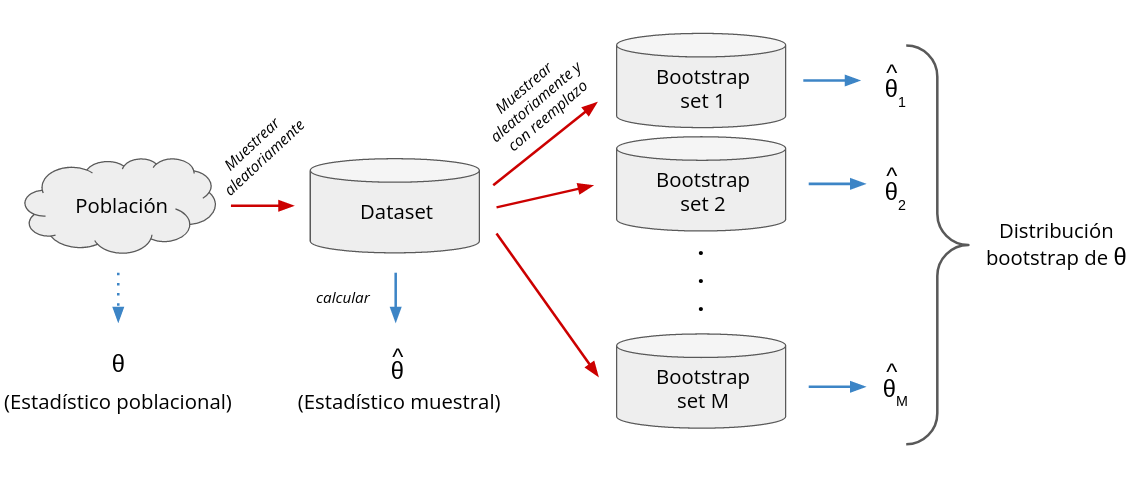
Digamos que contamos con un dataset \(\mathcal{D}\), que corresponde a una muestrea aleatoria de la población, y sobre el cual queremos evaluar un estadístico \(\theta\). El valor del estadístico sobre nuestro dataset es \(\hat \theta\).

Bootstrap nos permite obtener una distribución para el estadístico. El pseudo-código de bootstrap sería

Para \(j=1,2,3,\ldots,M\):

Obtener \(\mathcal{D}_j\) aplicando muestreo con reemplazo sobre \(\mathcal{D}\)
Calcular \(\hat \theta_j\) sobre \(\mathcal{D}_j\) y guardarlo

El conjunto de los \(M\) valores \(\hat \theta_j\) es la distribución bootstrap de \(\theta\). A mayor \(M\) mayor será el costo computacional y también la resolución de la distribución muestral.

Finalmente podemos usar la distribución bootstrap para

Calcular momentos estadísticos
Calcular percentiles y probabilidades
Obtener intervalos de confianza

y cualquier otro tipo de resumen o visualización que pudieramos hacer con una muestra

12.3. Intervalo de confianza con Bootstrap en Python¶

El módulo scipy.stats cuanta con una función llamada bootstrap que retorna intervalos de confianza utilizando el procedimiento descrito anteriormente

Sus principales argumentos son:

data: Un arreglo de numpy
statistic: Una función que recibe los datos y retorna un valor
n_resamples=9999: La cantidad de veces que se remuestrea el dataset (\(M\) en el diagrama anterior)
confidence_level=0.95: El nivel de confianza para calcular el intervalo de confianza

La función retorna un objeto namedtuple con el intervalo de confianza estimado mediante bootstrap y su error estándar

Veamos un ejemplo con un dataset generado sintéticamente

np.random.seed(12345)
data = ss.norm(loc=1, scale=1).rvs(100) # Datos simulados

Como estadístico de prueba utilizaremos

\[ \theta_1 \rightarrow \frac{1}{N} \sum_{i=1}^N x_i \]

es decir la media muestral.

Utilizaremos la implementación de NumPy para el estadístico con \(M=10000\) repeticiones

boot_result = ss.bootstrap((data,), statistic=np.mean,
                           confidence_level=0.95, n_resamples=10000, 
                           random_state=12345 # Por reprodubilidad
                          )
boot_result

BootstrapResult(confidence_interval=ConfidenceInterval(low=0.8329379739907918, high=1.2386119442343417), standard_error=0.10408824386103976)

Luego \(\theta \in [0.8329, 1.2386]\) con un 95% de confianza

Supongamos ahora que en lugar de la media nos interesa la distribución del siguiente estimador (totalmente arbitrario)

\[ \theta_2 \rightarrow \frac{1}{N} \sum_{i=1}^N x_i^2 (x_i - 1) \]

Para usar un estadístico personalizado sólo debemos definir una función que reciba el dataset y retorna el estadístico que nos interesa

def weird_statistic(data, axis=0):
    return np.mean(data**2*(data-1.), axis=axis)


boot_result = ss.bootstrap((data,), statistic=weird_statistic,
                           confidence_level=0.95, n_resamples=10000, 
                           random_state=12345 # Por reprodubilidad
                          )
boot_result

BootstrapResult(confidence_interval=ConfidenceInterval(low=1.3842499287450896, high=4.553871666786054), standard_error=0.6973363653977415)

12.4. Distribución Bootstrap en Python¶

En el ejemplo anterior vimos como obtener un intervalo de confianza con scipy.stats.bootstrap.

A continuación veremos una alternativa menos automática que nos retorna la distribución bootstrap completa del estadístico. La opción más simple es utilizar la función choice de NumPy para implementar el muestreo con reemplazo:

def bootstrap_resampling(data, random_state=None):
    np.random.seed(random_state)
    return np.random.choice(data, size=len(data), replace=True)

Luego aplicamos nuestro estadístico sobre las versiones remuestreadas del dataset original

En el siguiente ejemplo se usan 10.000 repeticiones y la implementación utiliza una comprensión del lista de Python

%%time
bootstrapped_statistic = np.array([np.mean(bootstrap_resampling(data)) for t in range(10000)])

CPU times: user 2.86 s, sys: 30.5 ms, total: 2.9 s
Wall time: 2.87 s

Ahora que tenemos la distribución completa podemos calcular resúmenes o crear visualizaciones a partir de ella. Por ejemplo un histograma:

bins, edges = np.histogram(bootstrapped_statistic, bins=20, density=True)

A continuación se muestra el histograma que acabamos de calcular

Nota

En este caso particular conocemos la distribución asintótica del estadístico (ver clase sobre máxima verosimilitud), por lo tanto podemos visualizarla junto al histograma

# Distribución muestral asintótica del MLE de la media de la distribución gaussiana
asymptotic_distribution = ss.norm(loc=np.mean(data), scale=1/np.sqrt(len(data)))
x = np.linspace(*asymptotic_distribution.ppf([0.001, 0.999]), num=200)
px = asymptotic_distribution.pdf(x)

p1 = hv.Histogram((edges, bins), kdims='x', vdims='Density', label='Bootstrap')
p2 = hv.Curve((x, px), label='Asintótica').opts(color='k')
p1 * p2

La distribución obtenida con bootstrap coincide bastante bien con la distribución muestral asintótica

También podemos utilizar la función de NumPy percentile sobre la distribución bootstrap para estimar el intervalo de confianza, obteniendo un resultado similar al que vimos anteriormente:

IC = np.percentile(bootstrapped_statistic, [2.5, 97.5])
print(f"Intervalo de confianza al 95%: {IC}")

Intervalo de confianza al 95%: [0.83324582 1.23328453]

Consideremos ahora el estadístico de prueba (arbitrario) que vimos anteriormente

\[ \theta_2 \rightarrow \frac{1}{N} \sum_{i=1}^N x_i^2 (x_i - 1) \]

Aplicando el mismo procedimiento anterior al nuevo estadístico

test_statistic = lambda data: np.mean(data**2*(data-1.))

bootstrapped_statistic = [test_statistic(bootstrap_resampling(data)) for t in range(10000)]

tenemos que su distribución muestral es:

bins, edges = np.histogram(bootstrapped_statistic, bins=20, density=True)
hv.Histogram((edges, bins), kdims='x', vdims='Density')

Nota

Para este estimador arbitrario (y para muchos otros) no hay distribución asintótica conocida. Estos son los casos donde bootstrap resulta sumamente valioso.

Importante

El poder de nuestro computadores nos permite implementar bootstrap para obtener distribuciones muestrales de estadísticos arbitrarios sin necesidad de imponer supuestos para la distribución subyacente (población).

Advertencia

Sin embargo los datos deben ser iid para que bootstrap sea valido. Si los datos son dependientes (e.g. series de tiempo) se deben usar otros tipos de remuestreos como por ejemplo block bootstrap.

Ver también

Para estudiar más a fondo las garantías de bootstrap recomiendo: http://www.stat.cmu.edu/~larry/=sml/Boot.pdf

Herramientas estadísticas para la investigación

Bootstrap no paramétrico

Contenido