9. Modelamiento parámetrico Bayesiano¶

9.1. Introducción¶

Cuando hacemos modelamiento bayesiano tenemos lo siguiente:

Los parámetros son variables aleatorias y tienen distribuciones de probabilidad
La distribución que siguen los parámetros antes de incorporar nuestras observaciones (datos) se llama prior
Inferir se refiere a aplicar el teorama de bayes para obtener el posterior de los parámetros

Para un vector de parámetros \(\theta\) y un dataset \(\{x\}\), usamos el teorema de Bayes y la ley de probabilidades totales para escribir:

\[ p(\theta| \{x\}) = \frac{p(\{x\}, \theta)}{p(\{x\})}= \frac{p(\{x\}|\theta) p(\theta)}{\int p(\{x\}|\theta) p(\theta) d\theta} \propto p(\{x\}|\theta) p(\theta), \]

Importante

El posterior se construye a partir de la verosimilitud \(p(\{x\}|\theta)\), el prior \(p(\theta)\) y la evidencia \(p(\{x\})\) (verosimilitud marginal). El posterior puede tener un valor bajo debido a que la verosimilitud es baja o que el prior es bajo.

¿Por qué y cuando debería usar el formalismo bayesiano?

En muchos casos la inferencia bayesiana no difiere mucho de las técnicas frecuentistas. Además, en general, la inferencia bayesiana es más costosa computacionalmente y requiere métodos más sofisticados.

Sin embargo lo anterior, el modelamiento bayesiano tiene algunas ventajas importantes

Tenemos no sólo el valor más probable sino también la incertidumbre de nuestros parámetros y predicciones: Podemos tomar decisiones más informadas
Podemos inyectar información de experimentos anteriores a través del prior, que además funciona como regularizador
Podemos integrar/marginalizar parámetros desconocidos (veremos esto en lecciones futuras)

Si cualquiera de los puntos anteriores fuera importante en nuestro problema, entonces valdrá la pena considerar el enfoque bayesiano

Inferencia bayesiana paso a paso

Formular el problema: Escribir verosimilitud y priors
Establecer la distribución conjunta (relaciones entre los parámetros)
Determinar el posterior con el teorema de Bayes. Como paso intermedio podemos buscar el MAP y la región creible
Evaluar nuestras hipótesis

En cada paso es important criticar, es decir discutir sobre que tan adecuado es el modelo y sugerir mejoras. A continuación veremos estos pasos en detalle.

9.2. Estimación de Maximo a posteriori (MAP)¶

En el caso bayesiano, el mejor estimador puntual de un parámetro está dado por el MAP:

\[ \hat \theta = \text{arg} \max_\theta p(\theta|\{x\}) = \text{arg} \max_\theta p(\{x\}| \theta) p(\theta), \]

Nota

La evidencia se omite porque no depende de \(\theta\)

Aplicando el logaritmo podemos separar la verosimilitud del prior

\[ \hat \theta = \text{arg} \max_\theta \log p(\{x\}| \theta) + \log p(\theta), \]

Importante

El MAP es un estimador puntual, sin embargo difiere del MLE ya que considera el prior

9.2.1. Priors y qué podemos hacer con ellos¶

Los priors son distribuciones que utilizamos para resumir lo que sabemos de antemano respecto del parámetro, por ejemplo

el parámetro es continuo y no tiene cotas
el parámetro es continuo y no-negativo
el parámetro es semi-definido positivo
el parámetro pertenece al simplex

¿Qué distribuciones conocidas puedes asociar a los puntos anteriores?

También podemos categorizar los priors como

Informativos: Son muy específicos respecto de donde el parámetro en cuestión es válido, e.g. \(\mathcal{N}(\theta|\mu=5.4, \sigma^2=0.1)\)
Débilmente informativo: Entregan información pero es más ambigüa que el caso anterior, e.g. \(\mathcal{N}(\theta|\mu=0, \sigma^2=100.)\)
No informativo o plano: No privilegia ningún valor por sobre otro, e.g. una distribución uniforme

Por supuestos, los términos y valores anteriores dependen del problema particular.

En general seleccionamos un prior tal que

le de un peso positivo a valores posibles del parámetro
le de peso cero a valores imposibles
contribuya a regularizar el modelo

Otro argumento conveniente desde el punto de vista computacional, es considerar un prior que sea conjugado con la verosimilitud que estamos utilizando. Veremos esto en detalle más adelante.

Ver también

Recomiendo encarecidamente leer la guía de principios prácticos para escoger priors de librería Stan (en inglés) y el capítulo 6 del libro “Bayesian Methods for Hackers”

9.2.2. Ejemplo: El MAP de la media de una distribución Gaussiana¶

Asumiendo que tenemos \(N\) datos i.i.d y una verosimilitud Gaussiana con variance conocida podemos escribir:

\[ \log p(\{x\}|\theta) = \log L (\mu) = - \frac{N}{2} \log 2\pi\sigma^2 - \frac{1}{2\sigma^{2}} \sum_{i=1}^N (x_i-\mu)^2, \]

Utilicemos por ejemplo un prior Gaussiano para \(\mu\) con parámetros \(\mu_0\) y \(\sigma_0\), esto sería:

\[ \log p(\theta) = -\frac{1}{2} \log 2 \pi \sigma^2_0 - \frac{1}{2 \sigma^2_0} (\mu - \mu_0)^2, \]

Luego derivamos el logaritmo de la distribución conjunta

\[ \frac{d}{d\mu} \log p(\{x\}|\theta) + \log p(\theta) = \frac{1}{\sigma^{2}} \sum_{i=1}^N (x_i-\mu) - \frac{1}{ \sigma^2_0} (\mu - \mu_0), \]

y lo igualamos a cero para obtener el MAP:

\[ \hat \mu_{\text{map}} = \left(\frac{N}{\sigma^2} + \frac{1}{\sigma^2_0} \right)^{-1} \left(\frac{N}{\sigma^2} \bar x + \frac{1}{\sigma^2_0} \mu_0 \right), \]

donde \(\bar x = \frac{1}{N} \sum_{i=1}^N x_i\).

Prudencia

No confunda \(\sigma^2\) con \(\sigma^2_0\), la primera representa la varianza de nuestros datos (ruido) mientras que la segunda representa la varianza de nuestro prior (incertidumbre)

Usando un poco de álgebra podemos escribir la expresión del MAP como:

\[\begin{split} \begin{split} \hat \mu_{\text{map}} &= \left(\frac{N}{\sigma^2} + \frac{1}{\sigma^2_0} \right)^{-1} \left(\frac{N\bar x}{\sigma^2} + \frac{\mu_0}{\sigma^2_0} \right) \\ &= \frac{N \bar x \sigma^2_0 + \mu_0 \sigma^2}{N\sigma^2_0+ \sigma^2} \\ &= \frac{\bar x + \mu_0 \frac{\sigma^2}{\sigma^2_0 N}}{1 + \frac{\sigma^2}{\sigma^2_0 N}} \\ &= w \bar x + (1-w) \mu_0, \qquad \text{where} \quad w = \frac{1}{1 + \frac{\sigma^2}{\sigma^2_0 N}} \end{split} \end{split}\]

Es decir que, el estimador MAP de \(\mu\) es una suma ponderada entre \(\bar x\) (la solución MLE) y \(\mu_0\) (la media del prior)

Nota

Si \(\sigma^2_0 \to \infty\) o \(N \to \infty\) entonces \(w \to 1\), i.e. el estimador MAP converge al MLE. El prior es más relevante cuando tenemos pocas muestras (\(N\) pequeño) o datos muy ruidosos (\(\sigma^2\) grande).

9.2.3. Conexión de la solución anterior con regularización¶

Podemos reescribir el problema de optimización anterior como

\[\begin{split} \begin{split} \hat \mu_{\text{map}} &= \text{arg} \max_\mu \log p(\{x\}| \mu, \sigma^2) + \log p(\mu) \\ &= \text{arg} \max_\mu - \frac{N}{2} \log 2\pi\sigma^2 - \frac{1}{2\sigma^{2}} \sum_{i=1}^N (x_i-\mu)^2 - \frac{1}{2\sigma_0^2} \mu^2 \\ &= \text{arg} \min_\mu \frac{1}{2\sigma^{2}} \sum_{i=1}^N (x_i-\mu)^2 + \frac{1}{2\sigma_0^2} \mu^2 \\ &= \text{arg} \min_\mu \|x-\mu\|^2 + \lambda \|\mu \|^2, \end{split} \end{split}\]

donde \(\lambda = \frac{\sigma^2}{\sigma_0^2}\).

Podemos reconocer la última ecuación como un problemas de mínimos cuadrados regularizado.

En este caso particular, utilizar un prior Gaussiano es equivalente a utilizar un regularizador de norma L2 sobre los parámetros. Esto se conoce como ridge regression
Utilizar un prior Laplaciano resulta en un regularizador de norma L1 sobre los parámetros 1

Revisaremos en profundidad este tema en el futuro.

9.3. Posterior analítico con priors conjugados¶

El MAP es sólo un estimador puntual. En inferencia Bayesiana estamos interesados en la distribución a posteriori completa

En el caso particular de la verosimilitud Gaussiana con prior Gaussiano podemos reordenar los términos como sigue:

\[\begin{split} \begin{split} p(\theta |\{x\}) &\propto p(\{x\} |\theta ) p(\theta ) \\ &\propto \exp \left ( \frac{1}{2\sigma^2} \sum_{i=1}^N (x_i - \mu)^2 \right) \exp \left ( \frac{1}{2\sigma_0^2} (\mu - \mu_0)^2 \right) \\ &\propto \exp \left ( -\frac{1}{2 \hat \sigma^2} (\mu - \hat \mu_{\text{map}} )^2 \right), \end{split} \end{split}\]

donde

\[ \hat \sigma^2 = \left(\frac{N}{\sigma^2} + \frac{1}{\sigma^2_0} \right)^{-1}, \]

i.e. el posterior tiene forma analítica cerrada y es también Gaussiano 2

Importante

Cuando el posterior resultante tiene la misma distribución que el prior que especificamos se dice que dicho prior es un prior conjugado con la verosimilitud especificada.

En este caso particular hemos mostrado que la distribución Gaussiana es conjugada consigo misma.

Otros ejemplos de priors conjugadas y sus respectivas verosimilitudes:

Tabla 9.1 Tabla de distribuciones conjugadas¶
Verosimilitud	Prior conjugado
Bernoulli	Beta
Poisson	Gamma
Multinomial o categorial	Dirichlet
Exponencial	Gamma
Gaussiana con varianza desconocida	Normal-inverse gamma (NIG)
Gaussiana multivariada con covarianza desconocida	Normal-inverse Wishart

Ejemplo interactivo

A continuación se genera una muestra Gaussiana con media \(\mu=2\) y \(\sigma=1\). Comparemos graficamente la

(amarillo) distribución asintótica del estimador de máxima verosimilitud
(rojo) posterior analítico
(azul) prior

para esta muestra. A continuación se implementa las rutinas necesarias:

from scipy.stats import norm

def mle_mu(xi: np.array) -> float:
    return np.mean(xi)

def asymptotic_mle(x: np.array, xi: np.array, s2: float) -> np.array:
    N = len(xi)
    return norm(loc=mle_mu(xi), scale=np.sqrt(s2/N)).pdf(x)

def map_mu(xi: np.array, mu0: float, s20: float, s2: float):
    N = len(xi)
    w = (N*s20)/(N*s20 + s2)
    return mle_mu(xi)*w + mu0*(1. - w) 

def prior_mu(x: np.array, mu0: float, s20: float) -> np.array:
    return norm(loc=mu0, scale=np.sqrt(s20)).pdf(x)

def posterior_mu(x: np.array, xi: np.array, mu0: float, s20: float, s2: float) -> np.array:
    N = len(xi)
    s2_pos = s2*s20/(N*s20 + s2)
    mu_pos = map_mu(xi, mu0, s20, s2)
    return norm(loc=mu_pos, scale=np.sqrt(s2_pos)).pdf(x)

Utilice la interfaz para responder las siguientes preguntas

¿Qué ocurre cuando \(N\) (el tamaño de la muestra) crece?
¿Qué ocurre cuando \(\sigma_0\) (la varianza del prior) crece?

mu_real, s2_real = 2., 1.
x_plot = np.linspace(-5, 5, num=1000)
true_value = hv.VLine(mu_real).opts(color='k', line_width=2, alpha=0.5)
hmap = hv.HoloMap(kdims=['N', 'mu0', 's20'])
for N in [1, 5, 10, 50, 100, 500]:
    for mu0 in np.linspace(-3, 3, num=5):
        for s20 in np.logspace(-1, 1, num=3):
            data = norm(loc=mu_real, scale=np.sqrt(s2_real)).rvs(N, random_state=1234)
            plot_prior = hv.Curve((x_plot, prior_mu(x_plot, mu0, s20)), 'x', 'density', label='prior') 
            plot_mle = hv.Curve((x_plot, asymptotic_mle(x_plot, data, s2_real)), label='MLE')
            plot_post = hv.Curve((x_plot, posterior_mu(x_plot, data, mu0, s20, s2_real)), label='posterior')
            hmap[(N, mu0, s20)] = (plot_prior * plot_post * plot_mle * true_value).opts(hv.opts.Curve(width=500))
            
hmap

9.3.1. Prior conjugado para verosimilitud Gaussiana con varianza desconocida¶

Anteriormente asumimos que \(\sigma^2\) era una cantidad conocida y nos enfocamos en estimar \(\mu\). Consideremos el caso contrario, i.e. donde la media es conocida y queremos estimar la varianza.

En dicho caso el prior conjugado de la verosimilitud Gaussiana es la distribución gamma inversa (Inverse Gamma, IG):

\[ p(\sigma^2) = \text{IG}(\alpha_0, \beta_0) = \frac{\beta_0^{\alpha_0}}{\Gamma(\alpha_0)} x^{-\alpha_0-1} e^{-\frac{\beta_0}{x}} \]

Y por lo tanto el posterior resultante es también gamma inverso, \(p(\sigma^2|\{x\}) = \text{IG}\left(\alpha_N , \beta_N \right)\), con parámetros:

\( \alpha_N = \alpha_0 + N/2\)
\(\beta_N = \beta_0 + \frac{1}{2} \sum_{i=1}^N (x_i - \mu)^2\)

9.3.2. Prior conjugado para la verosimilitud Gaussiana cuando ningún parámetro es conocido¶

Simplemente multiplicar un prior Gaussiano para \(\mu\) con un prior Gamma inverso para \(\sigma\) no resulta en un prior conjugado que es conjugado. Se debe considerar que los parámetros \(\mu\) y \(\sigma\) no son independientes como muestra el siguiente modelo jerárquico:

\[\begin{split} \begin{split} p(x_i|\mu, \sigma^2) &= \mathcal{N}(\mu, \sigma^2) \\ p(\mu|\sigma^2) &= \mathcal{N}(\mu_0, \sigma^2/\lambda_0) \\ p(\sigma^2) &= \text{IG}(\alpha, \beta) \end{split} \end{split}\]

La distribución a priori conjunta de \(\mu\) y \(\sigma\) se llama normal-inverse-gamma (NIG) y tiene cuatro parámetros:

\[ p(\mu, \sigma^2) = \text{NIG}(\mu_0, \lambda_0, \alpha_0, \beta_0) = \mathcal{N}(\mu_0 , \sigma^2/\lambda_0) \text{IG}(\alpha_0, \beta_0) \]

Cuando se tiene verosimilitud Gaussiana y prior NIG el posterior resultante también es NIG:

\[ p(\mu, \sigma^2|\{x\}) = \text{NIG}(\mu_n, \lambda_n, \alpha_n, \beta_n) \]

donde

\(\lambda_n = \lambda_0 + N\)
\(\mu_n = \lambda_n^{-1} \left ( \lambda_0 \mu_0 + N \bar x \right)\)
\(\alpha_n = \alpha_0 + N/2\)
\(\beta_n = \beta_0 + 0.5\mu_0^2\lambda_0 + 0.5\sum_i x_i^2 - 0.5\lambda_n \mu_n^2\)

9.4. Describiendo un posterior bayesiano¶

En esta sección se presenten resúmenes típicamente utilizados para resumir y describir un posterior. El descriptor más básico de un posterior es su localización o moda, es decir el MAP.

También es interesante resumir la incertidumbre en torno a la moda, lo cual se hace midiendo el “ancho” del posterior. Sea un parámetro \(\theta\), llamamos intervalo de credibilidad (*Credible Interval, CI) a la región contigua \([\theta_{l}, \theta_{u}]\) tal que

\[ P(\theta_{l}< \theta < \theta_{u}) = 1 - \alpha \]

donde si \(\alpha=0.05\), entonces el CI será al 95%. En el caso de un posterior analítico este intervalo se puede calcular facilmente con los percentiles de la distribución, como muestra el ejemplo más abajo.

La región de mayor densidad (Highest Posterior Density Region, HPD o HPR), es una alternativa al CI que es más adecuada si el posterior tiene múltiples modas. El HPD depende no sólo del ancho para también de la altura del posterior.

La siguiente figura muestra la diferencia entre el CI y el HPD para un posterior multi-modal:

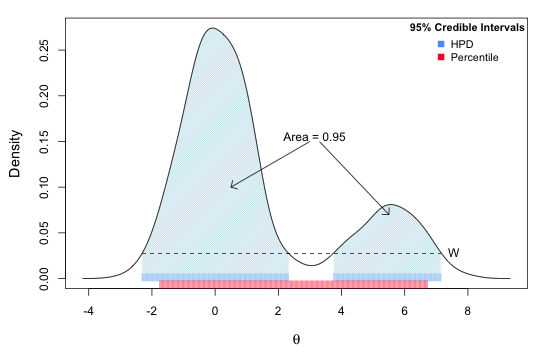
Ejemplo

El CI al 95% de \(\mu\) con \(\sigma^2\) conocido en función de \(N\) es:

mu0, s20 = 0., 10.

for N in [10, 100, 1000]:
    data = norm(loc=mu_real, scale=np.sqrt(s2_real)).rvs(N, random_state=12345)
    s2_pos = s2_real*s20/(N*s20 + s2_real)
    mu_pos = map_mu(data, mu0, s20, s2_real)
    dist = norm(loc=mu_pos, scale=np.sqrt(s2_pos))
    display(f'95% CI for mu, N={N}: [{dist.ppf(0.025):0.4f}, {dist.ppf(0.975):0.4f}]')

'95% CI for mu, N=10: [1.8534, 3.0869]'

'95% CI for mu, N=100: [1.8357, 2.2275]'

'95% CI for mu, N=1000: [1.9355, 2.0594]'

9.5. Qué hacer si el posterior no tiene forma analítica¶

En esos casos se utilizan métodos aproximados como inferencia variacional o métodos basados en Markov Chain Monte Carlo (MCMC), los cuales veremos en lecciones futuras

1: Hastie, Tibshirani, Friedman, chapter 3.4 (Shrinkage methods), page 61.
2: Otra forma de mostrar que el posterior resultante es Gaussiano es utilizar la propiedad de multiplicación de Gaussianas

Herramientas estadísticas para la investigación

Modelamiento parámetrico Bayesiano

Contenido

9. Modelamiento parámetrico Bayesiano¶

9.1. Introducción¶

9.2. Estimación de Maximo a posteriori (MAP)¶

9.2.1. Priors y qué podemos hacer con ellos¶

9.2.2. Ejemplo: El MAP de la media de una distribución Gaussiana¶

9.2.3. Conexión de la solución anterior con regularización¶

9.3. Posterior analítico con priors conjugados¶

9.3.1. Prior conjugado para verosimilitud Gaussiana con varianza desconocida¶

9.3.2. Prior conjugado para la verosimilitud Gaussiana cuando ningún parámetro es conocido¶

9.4. Describiendo un posterior bayesiano¶

9.5. Qué hacer si el posterior no tiene forma analítica¶