20. Modelamiento Bayesiano¶

En el enfoque Bayesiano:

La inferencia se realiza calculando la distribución a posteriori de los parámetros
Se modela la incerteza de los datos y parámetros con una distribución de probabilidad conjunta
$\theta$ es un vector aleatorio cuya distribución de probabilidad se denomina a priori

El teorema de Bayes y la ley de probabilidades totales nos permiten escribir:

\[p(\theta| \cal{D}) = \frac{p(\cal{D}, \theta)}{p(\cal{D})}= \frac{p(\cal{D}|\theta) p(\theta)}{\int p(\cal{D}|\theta) p(\theta) d\theta} \propto p(\cal{D}|\theta) p(\theta),\]

En el enfoque Bayesiano buscamos calcular la distribución a posteriori, la que se construye a partir de la función de verosimilitud, la distribución a priori y la evidencia, conocida también como la verosimilitud marginal de los datos.

20.1. El procedimiento de inferencia Bayesiana:¶

Definir la función de verosimilitud de los datos
Escoger una distribución a priori para los parámetros
Construir la distribución conjunta de datos y parámetros
Determinar la distribución a posteriori usando el Teorema de Bayes
Calcular estimadores puntuales

20.1.1. Estimadores puntuales¶

Moda a posteriori (MAP, maximum a posteriori)

\[\hat \theta = \text{arg} \max_\theta p(\theta|\cal{D}) = \text{arg} \max_\theta p(\cal{D}| \theta) p(\theta),\]

para esta maximización no se requiere la evidencia pues esta no depende de $\theta$. Además aplicando logaritmo podemos separar la verosimilitud de la distribución a priori:

\[\hat \theta = \text{arg} \max_\theta (\log p(\cal{D}| \theta) + \log p(\theta)),\]

Esperanza a posteriori

\[\mathbb{E}(\theta \mid \cal{D}) = \int \theta p(\theta \mid \cal{D}) d\theta\]

Varianza a posteriori

\[\mathbb{V}(\theta \mid \cal{D}) = \int (\theta- \mathbb{E}(\theta \mid \cal{D}))^2 p(\theta \mid \cal{D}) d\theta\]

Algunas dificultades con MAP:

no es necesariamente representativa de la distribución a posteriori
no es invariante a reparametrizaciones de los parámetros

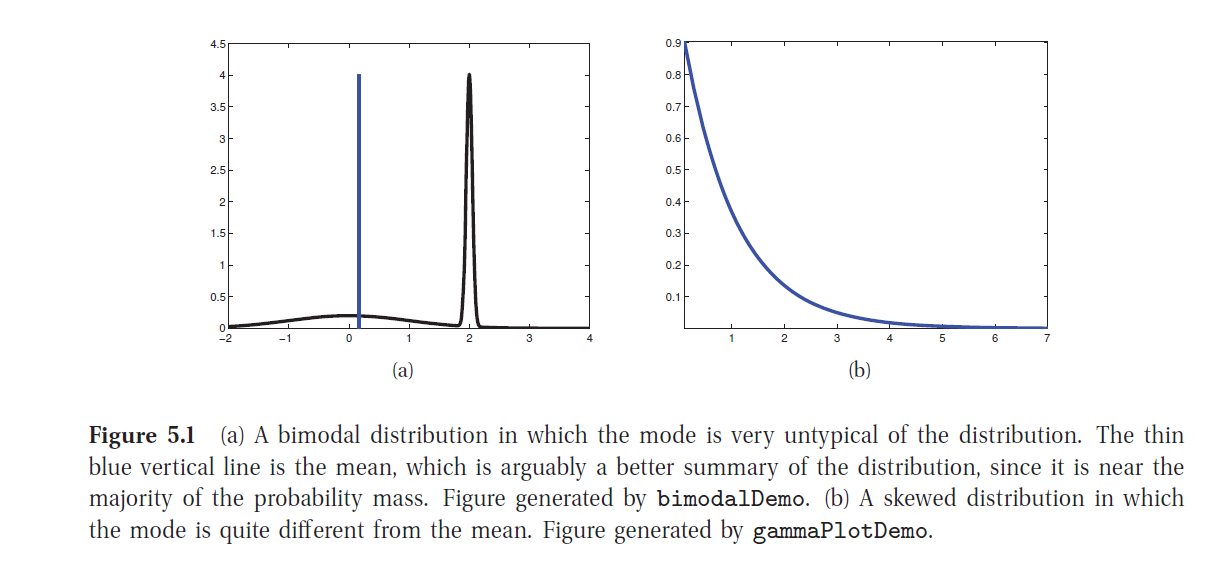
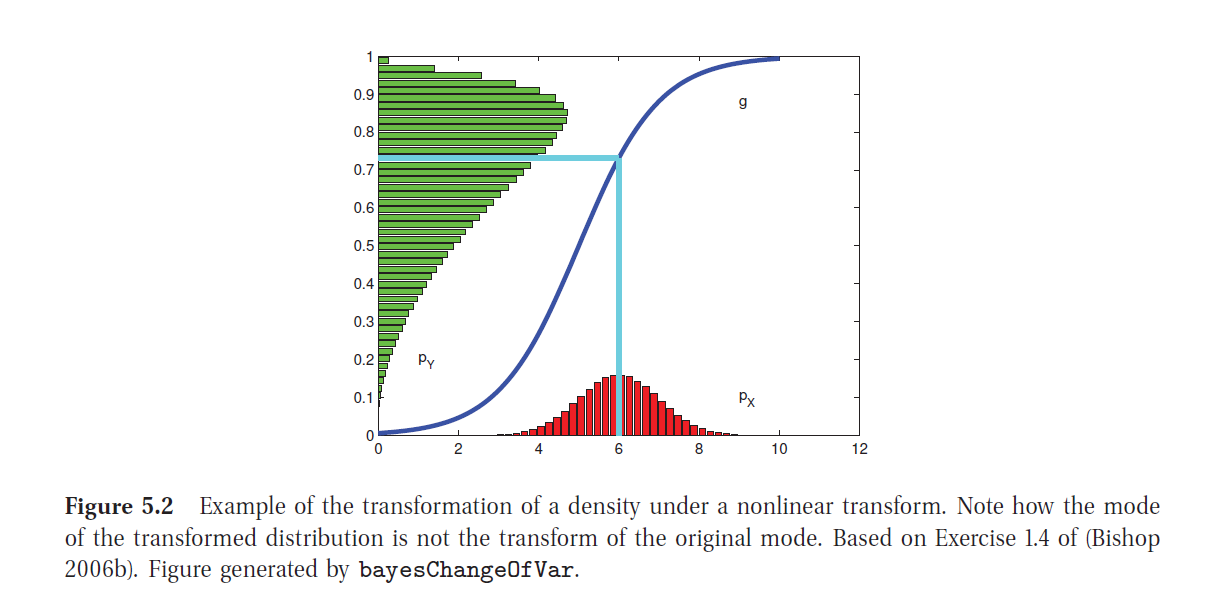
20.1.2. Intervalos de credibilidad:¶

Intervalos centrales

\[C_{\alpha}({\cal D}) = (l,u) : P(l \leq \theta \leq u \mid {\cal D}) = 1-\alpha\]

Regiones de mas altas densidades a posteriori (HPD):

Sea $p*$ un umbral para la distribución a posteriori que cumple que:

\[1-\alpha = \int_{\theta: p(\theta\mid {\cal D})>p*} p(\theta \mid {\cal D}) d\theta\]

entonces se define:

\[C_{\alpha}({\cal D}) = \{ \theta : p(\theta\mid {\cal D})\geq p*\}\]

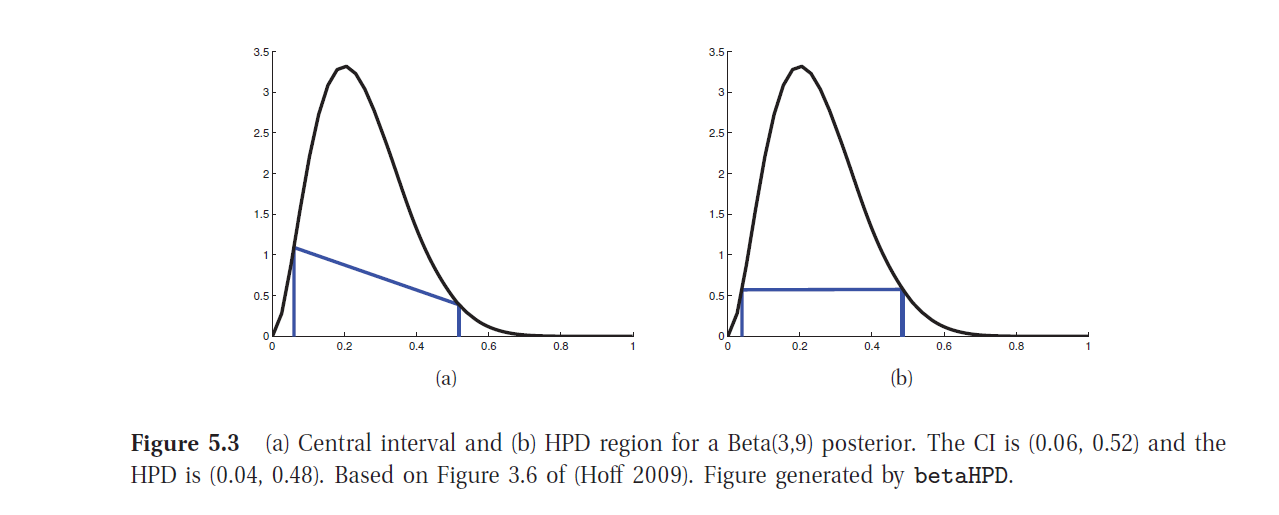
Distribución Predictiva a posteriori

\[p(x \mid \cal{D}) = \int p(x \mid \theta) p(\theta \mid \cal{D}) d\theta\]

Nos permite predecir la probabilidad de ocurrencia de un nuevo dato $x$

20.2. Distribuciones naturales conjugadas¶

Una elección posible para las distribuciones a priori son aquellas que se conjugan con las funciones de verosimilitud, de manera que la distribución a posteriori es del mismo tipo que la distribución a priori pero con nuevos parámetros. Veamos algunos ejemplos.

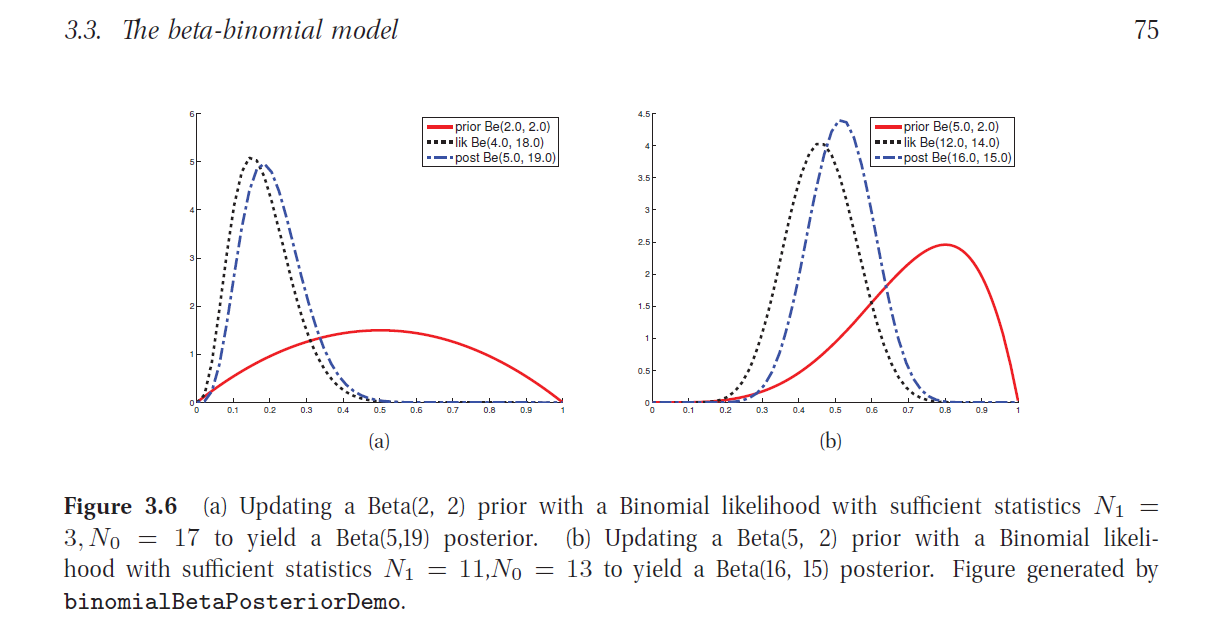
20.2.1. El modelo Beta-binomial¶

Consideremos el caso en que

\[ X_i \sim i.i.d. \, Binomial(K,\theta) \qquad X_i \in \{0,...,K\}, i=1,\cdots,n\]

\[ P(X_i = k\mid \theta) = {{K}\choose{k}} \theta^k (1-\theta)^{(K-k)} \qquad k = 1,...,K\]

Y por otra parte

\[ \theta \sim Beta(a,b) \qquad \theta \in [0,1], a,b>0\]

\[f_{\theta}(\theta) = \frac{\Gamma(a+b)}{ \Gamma(a) \Gamma(b)} \theta^{a-1} (1-\theta)^{b-1} \qquad \theta \in [0,1]\]

suppressMessages(library(dplyr))
suppressMessages(library(plotly))
suppressMessages(library(ggplot2))
suppressMessages(library(rmarkdown))

vec <- seq(0,1,by=0.01)
params <- c(0.1,0.5,1,2,3,4,5,6,7,8)

pvec <- list()
for (i in 1:length(params))
    for (j in 1:length(params)){
        k = length(params)*(i-1) + j
        pvec[[k]] <- dbeta(vec,params[i],params[j])
}

steps <- list()

fig <- plot_ly(width=600,height=600) %>% layout(title = "\n \n Densidad de Probabilidad Beta, a=0.1")


     
i=1
     for (j in 1:length(params)){
        k <- length(params)*(i-1) + j
        fig <- add_lines(fig, x=vec, y=pvec[[k]], 
                     visible=if ((i==1) && (j==1)) TRUE else FALSE,
                     mode='lines', line=list(color='blue'), showlegend=FALSE)
       step <- list(args = list('visible', rep(FALSE, length(params))), 
                    method='restyle',label=params[j])
       step$args[[2]][j] <- TRUE
       steps[[j]] <-step                 
}


fig <- fig %>% layout(sliders = 
                      list( list(active=0, 
                                currentvalue = list(prefix = "b: "),
                                pad = list(t=10),
                                steps=steps)))
fig

steps <- list()

fig <- plot_ly(width=600,height=600) %>% layout(title = "\n \n Densidad de Probabilidad Beta, a=1")


     
i=3
     for (j in 1:length(params)){
        k <- length(params)*(i-1) + j
        fig <- add_lines(fig, x=vec, y=pvec[[k]], 
                     visible=if ((i==3) && (j==1)) TRUE else FALSE,
                     mode='lines', line=list(color='blue'), showlegend=FALSE)
       step <- list(args = list('visible', rep(FALSE, length(params))), 
                    method='restyle',label=params[j])
       step$args[[2]][j] <- TRUE
       steps[[j]] <-step                 
}


fig <- fig %>% layout(sliders = 
                      list( list(active=0, 
                                currentvalue = list(prefix = "b: "),
                                pad = list(t=10),
                                steps=steps)))
fig

steps <- list()

fig <- plot_ly(width=600,height=600) %>% layout(title = "\n \n Densidad de Probabilidad Beta, a=8")


     
i=10
     for (j in 1:length(params)){
        k <- length(params)*(i-1) + j
        fig <- add_lines(fig, x=vec, y=pvec[[k]], 
                     visible=if ((i==10) && (j==1)) TRUE else FALSE,
                     mode='lines', line=list(color='blue'), showlegend=FALSE)
       step <- list(args = list('visible', rep(FALSE, length(params))), 
                    method='restyle',label=params[j])
       step$args[[2]][j] <- TRUE
       steps[[j]] <-step                 
}


fig <- fig %>% layout(sliders = 
                      list( list(active=0, 
                                currentvalue = list(prefix = "b: "),
                                pad = list(t=10),
                                steps=steps)))
fig

Algunas Propiedades de la Distribución Beta

i) $moda(\theta)= \underset{\theta}{\operatorname{argmax}} f_{\theta}(\theta)$

\[\begin{split}\begin{align} \frac{\partial f_{\theta}(\theta)}{\partial \theta}=0 \qquad &\implies \qquad (a-1)\theta^{a-2}(1-\theta)^{b-1} - (b-1)\theta^{a-1}(1-\theta)^{b-2} =0 \nonumber\\ &\implies \qquad \theta^{a-2}(1-\theta)^{b-2}((a-1)(1-\theta) - (b-1)\theta) =0 \nonumber\\ &\implies \qquad \theta(a-1 + b-1) =a-1 \nonumber\\ &\implies \qquad moda(\theta) = \frac{a-1}{a+b-2} \nonumber\\ \end{align}\end{split}\]

ii) $\mathbb{E}(\theta) = \int_0^1 \theta f_{\theta}(\theta) d\theta$

\[\begin{split}\begin{align} \mathbb{E}(\theta) & = \frac{\Gamma(a+b)}{ \Gamma(a) \Gamma(b)} \int_0^1 \theta \theta^{a-1} (1-\theta)^{b-1}d\theta \nonumber\\ & = \frac{a}{a+b} \nonumber\\ \end{align}\end{split}\]

iii) $\mathbb{V}(\theta) = \int_0^1 (\theta- \mathbb{E}(\theta)^2 f_{\theta}(\theta) d\theta$

\[\begin{split}\begin{align} \mathbb{V}(\theta) & = \frac{\Gamma(a+b)}{ \Gamma(a) \Gamma(b)} \int_0^1 (\theta- \mathbb{E}(\theta)^2 \theta^{a-1} (1-\theta)^{b-1}d\theta \nonumber\\ & = \frac{ab}{(a+b)^2(a+b+1)} \nonumber\\ \end{align}\end{split}\]

Nota:

\[\Gamma(z) = \int_0^{\infty} t^{z-1} e^{-t} dt\]

y cumple:

\[\Gamma(z+1) = z \Gamma(z), \qquad \Gamma(n) = (n-1)! , n\in N\]

Cálculo de la distribución a posteriori

\[\begin{split} \begin{align} f_{\theta}(\theta \mid \{X_i\}) &\propto \prod_{i=1}^n P(X_i=k_i\mid \theta)f_{\theta}(\theta) \nonumber \\ &\propto \prod_{i=1}^n \theta^{k_i} (1-\theta)^{(K-k_i)} \theta^{a-1} (1-\theta)^{b-1} \nonumber \\ &\nonumber\\ &= \theta^{N_1} (1-\theta)^{N_0} \theta^{a-1} (1-\theta)^{b-1} \nonumber \\ & \nonumber\\ &= \theta^{N_1+a-1} (1-\theta)^{N_0+b-1} \end{align} \end{split}\]

donde

\[N_1 = \sum_{i=1}^n k_i \qquad y \qquad N_0 = \sum_{i=1}^n (K-k_i)\]

Es decir

\[ \theta \mid \{X_i\}_{i=1,..,n} \sim Beta(N_1+a,N_0+b)\]

Moda a posteriori (MAP):

\[\theta_{MAP}= \underset{\theta}{\operatorname{argmax}} f_{\theta}(\theta \mid \{x_i\})= \frac{a+N_1-1}{a+b+N-2}\]

Media a posteriori:

\[\mathbb{E}(\theta \mid \{x_i\}_{i=1,...,n}) = \frac{a+N_1}{a+b+N}\]

Varianza a posteriori

\[\mathbb{V}(\theta \mid \{x_i\}_{i=1,...,n}) = \frac{(a+N_1)(b+N_2)}{(a+b+N)^2(a+b+N+1)}\]

# parámetros a priori: Beta(5,2)
# parámetros likelihood: Beta(n1+1,n0+1)
# parametros a posteriori: Beta(5+n1,2+n0)
a=5
b=2
N=20
vec <- seq(0,1,by=0.01)
pvec0 <- dbeta(vec,a,b)
params <- seq(0,N,by=1)
params <- c(rbind(params,params))
aval <- list()


for (i in 1:length(params)){
      aval[[i]] <-list(visible = FALSE,
                      y=dbeta(vec,params[i]+1,(N-params[i])+1),
                      z=dbeta(vec,params[i]+a,(N-params[i])+b))
                      
}

steps <- list()
fig <- plot_ly(width=600,height=400) %>% layout(title = "\n \n Modelo Beta-Binomial", yaxis = list(range=c(0,8))) %>%
        add_lines(x=vec,y=pvec0,line=list(color='red'),name= "Prior Beta(5,2)",showlegend=TRUE)
        
for (i in 1:N){
    
   fig <- add_lines(fig,x=vec,  y=aval[[2*i]]$y, visible = aval[[2*i]]$visible,
                    type = 'scatter', mode = 'lines', line=list(color='black',dash='dot'), name= "Likelihood")
    
   fig <- add_lines(fig,x =vec, y=aval[[2*i]]$z ,visible = aval[[2*i]]$visible,
                    type = 'scatter', mode = 'lines', line=list(color='blue',dash='dash'),name = "Posterior")
   
  step <- list(args = list('visible', rep(FALSE, 2*length(aval)+3)),
               method = 'restyle',label=i)
  step$args[[2]][2*i] = TRUE
  step$args[[2]][2*i+1] = TRUE  
  step$args[[2]][1] = TRUE
  steps[[i]] = step 
  
}  
length(steps)


# add slider control to plot
fig <- fig %>%
  layout(sliders = list(list(active = 1,
                             currentvalue = list(prefix = "N_1: "),
                             steps = steps)))
                             
fig

20

20.2.2. El modelo Dirichlet-multinomial¶

Consideremos el caso en que

\[{\bf{X}}=(x_1,\cdots,x_K) \sim Multinomial(n,{\bf{\theta}}) \qquad 0\leq x_i \leq n,\,\, n=\sum_{k=1}^K x_k, \,\,{\bf{\theta}}=(\theta_1,\cdots, \theta_K)\]

\[ P(X = (x_1,\cdots,x_k) \mid {\bf{\theta} }) = {{n}\choose{x_1,\cdots,x_k}}\prod_{k=1}^K\theta_k^{x_k} = \frac{n!}{x_1!\cdots x_k!}\prod_{k=1}^K\theta_k^{x_k}\]

De manera que la función de verosimilitud para n observaciones queda:

\[ P(\cal{D} \mid \bf{\theta}) \propto \prod_{k=1}^K\theta_k^{N_k}\]

donde

\[N_k = \sum_{i=1}^n (X_i)_k\]

Por otra parte, sea

\[ \theta = (\theta_1,\cdots\theta_K) \sim Dirichlet(\alpha_1,\cdots,\alpha_K) \qquad \theta_i \in [0,1], \sum_{k=1}^K \theta_i= 1, \alpha_i>0\]

\[f_{\theta}(\theta) = \frac{1}{B(\alpha)} \prod_{k=1}^K \theta_k^{\alpha_k-1} \qquad B(\alpha) = \frac{\prod_{k=1}^K \Gamma(\alpha_k)}{\Gamma(\alpha_1+\cdots+\alpha_K)}\]

En este caso, resulta que la distribución a posteriori es también Dirichlet:

\[\begin{split} \begin{align} f_{\theta}(\theta \mid \cal{D}) & \propto P(\cal{D} \mid \theta)f_{\theta}(\theta) \nonumber \\ & \propto \prod_{k=1}^K \theta_k^{N_k}\theta_k^{\alpha_k-1} = \prod_{k=1}^K \theta_k^{N_k+\alpha_k-1} \nonumber \end{align} \end{split}\]

Es decir

\[(\theta \mid {\cal{D}}) \sim Dirichlet(\alpha_1+N_1,\cdots,\alpha_K+N_k)\]

Ejemplo: diferencia de proporciones

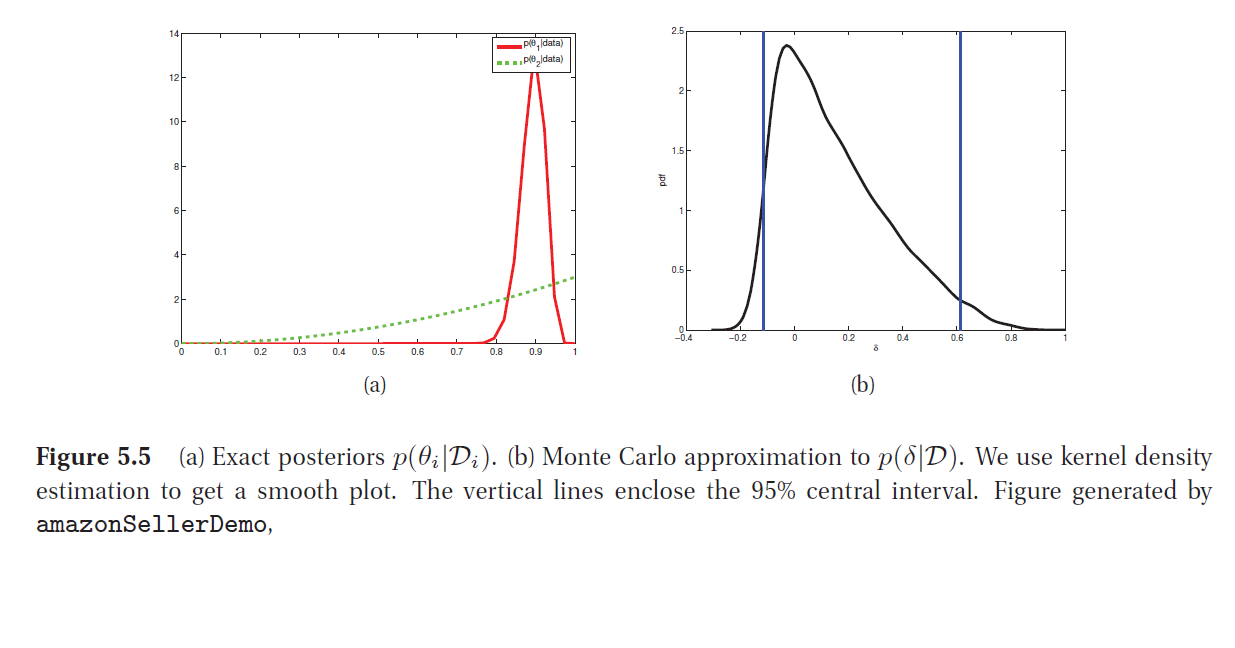
Supongamos que estamos interesados en comprar en una plataforma online, y hay dos vendedores que entregan el producto al mismo precio. El vendedor 1 tiene 90 evaluaciones positivas y 10 negativas. El vendendor 2 tiene 2 evaluaciones positivas y 0 negativas. ¿Cómo decidir cual comprar? En el enfoque bayesiano, el análisis es como sigue:

Sean $\theta_1$ y $\theta_2$ las confiabilidades reales de los dos vendedores. Como no tenemos mas información, vamos a considerar a priori uniformes: $\theta_i \sim Beta(1,1)$ y entonces podemos usar el modelo beta-binomial. De manera que

\[\theta_i \mid {\cal D} \sim Beta(1+y_i, 1 + N_i - y_i), \qquad i=1,2\]

En este caso $$N_1 = 100, \,y_1 = 90,\qquad N_2 = 2,\, y_2 =2$$

Entonces podemos calcular, para $\delta = \theta_1 - \theta_2$:

\[P(\delta > 0 \mid {\cal D}) = \int_0^1 \int_0^1 \mathbb{1}_{\{\theta_1 - \theta_2>0\} }Beta(1+y_1, 1 + N_1 - y_1)\]

\[\qquad \qquad \qquad \qquad Beta(1+y_2, 1 + N_2 - y_2)d\theta_1 d\theta_2\]

Utilizando integración numérica se puede obtener que $P(\delta > 0 \mid {\cal D})= 0.71$ y un intervalo central de la figura.

20.3. Enfoque Bayesiano para la Selección de modelos¶

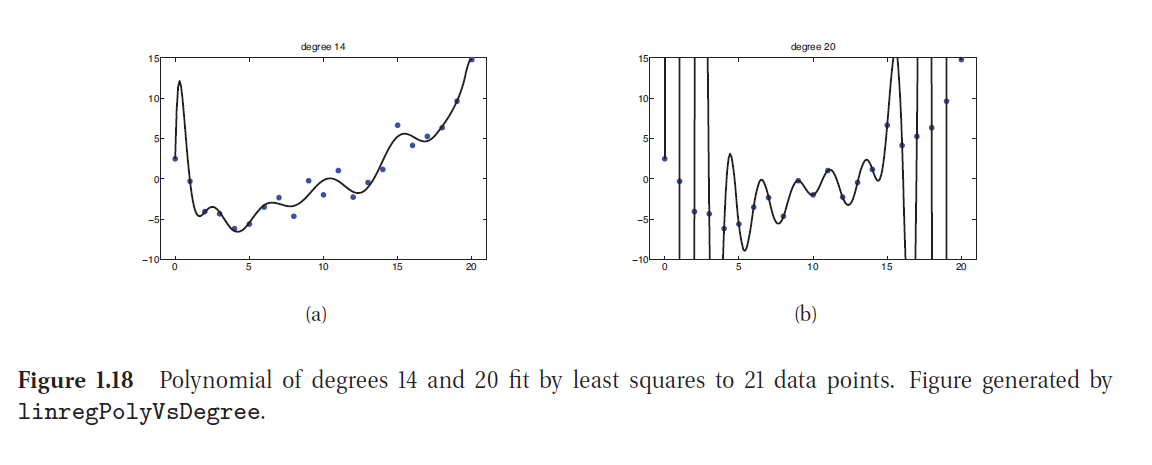
Si disponemos de un conjunto de modelos entre los cuales elegir, por ejemplo una familia de distribuciones de probabilidad paramétricas de complejidad diferente, estamos en presencia del problema de selección de modelos.

En el enfoque frecuentista, una manera de abordar esto es usar validación cruzada (cross-validation), para definir los errores para cada modelo y luego seleccionar el de mínimo error.

En el enfoque Bayesiano podemos hacer uso de la distribución predictiva de los datos o evidencia, por cada modelo $m$ y escoger el de mayor probabilidad dados los datos $\cal{D}$

\[p(m \mid \cal{D}) = \frac{p(\cal{D} \mid m) p(m) }{\sum_{m \in \cal{M}}p(\cal{D} \mid m) p(m)}\]

y entonces calculamos el modelo MAP:

\[\hat{m} = \underset{m \in \cal{M}}{\operatorname{argmax}}p(m \mid \cal{D})\]

Si consideramos una distribución a priori no informativa sobre los modelos (distribución uniforme), es decir $p(m) \propto 1$, tenemos que:

\[p(m \mid \cal{D}) \propto p(\cal{D} \mid m) = \int p(\cal{D} \mid \theta) p(\theta \mid m) d\theta\]

llamada verosimilitud marginal o evidencia del modelo $m$.

La navaja de Occam: (Bayesian Occam’s razor): el hecho de que la verosimilitud marginal considere la integración respecto de los parámetros impide que se maximice simplemente por aumentar el número de parámetros, con lo cual se previene el sobreajuste en la elección del modelo.

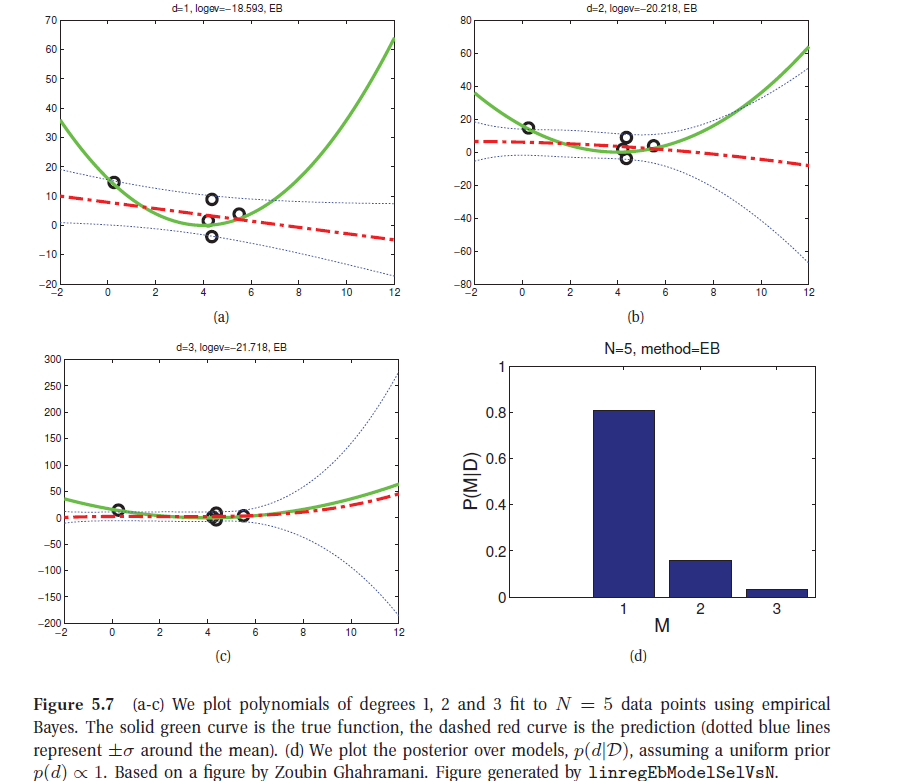
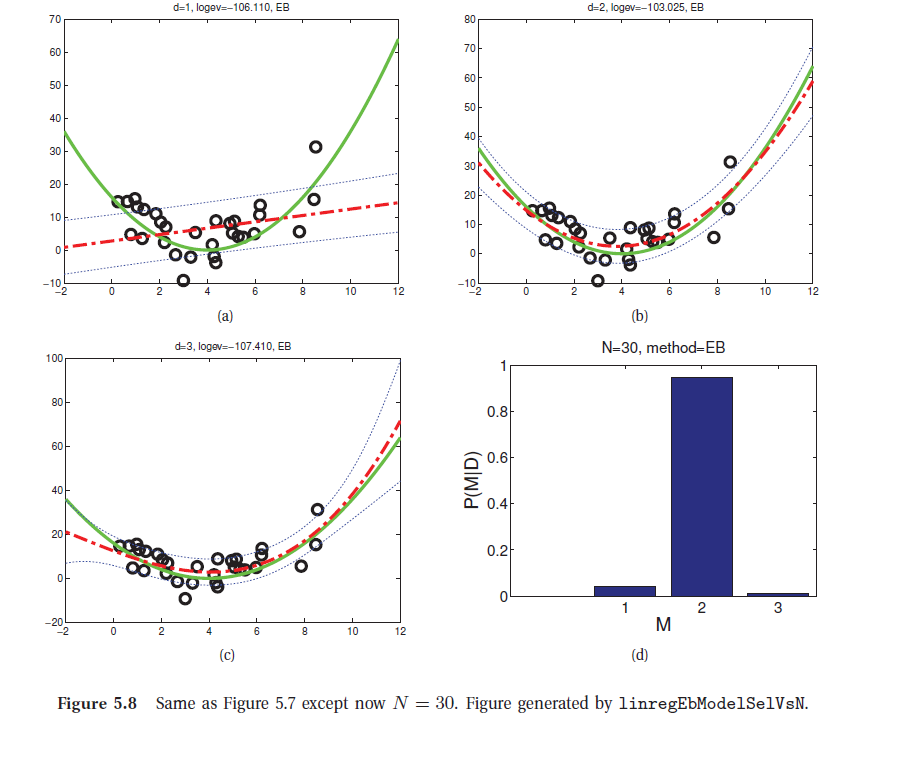
El cálculo de la verosimilitud marginal o evidencia es computacionalmente costoso en general y requiere utilizar técnicas del tipo Monte Carlo, salvo cuando tratamos con modelos de distribuciones conjugadas.

Veamos el caso del modelo Beta-Binomial:

En esta caso

\[\cal{M} = \{ m_{a,b} \mid \theta \sim Beta(a,b), a,b>0 \}\]

Para el cálculo de $p(\cal{D} \mid m)$, recordemos que en este caso la distribución a posteriori se distribuye $Beta(a+N_1,b+N_0)$, entonces considerando Bayes tenemos:

\[\begin{split} \begin{align} p(\cal{D} \mid m) &= \frac{p(\cal{D} \mid \theta, m) p(\theta \mid m)}{p(\theta \mid \cal{D},m)} \nonumber \\ &\\ &= \frac{\left({{N}\choose{N_1}}\theta^{N_1-1}(1-\theta)^{N_0-1}\right)\left( \frac{1}{B(a,b)}\theta^{a-1}(1-\theta)^{b-1}\right)} {\left(\frac{1}{B(a+N_1,b+N_0)}\theta^{a+N_1-1}(1-\theta)^{b+N_0-1}\right)}\\ &\\ &= {{N}\choose{N_1}} \frac{B(a+N_1,b+N_0)}{B(a,b)} \end{align} \end{split}\]

20.3.1. Aproximación BIC del logaritmo de la verosimilitud marginal¶

Considerando que el cálculo de la verosimilitud marginal es en general costoso, Schwartz(1978) propone el Criterio de Información Bayesiano (BIC), como una aproximación del logaritmo de la verosimilitud marginal:

\[BIC = log p(\cal{D} \mid \hat{\theta}) -\frac{dof(\hat{\theta})}{2} log {\text N} \approx \log p(\cal{D})\]

donde $dof(\hat{\theta})$ son los grados de liberdad del modelo y $\hat{\theta}$ es el estimador de máxima verosimilitud de $\theta$.

De esta manera el BIC se puede interpretar como una versión del logaritmo de la verosimilitud penalizada por la complejidad del modelo.

Herramientas estadísticas para la investigación

Modelamiento Bayesiano

Contenido