Análisis Exploratorio y Reducción de la Dimensionalidad
Contenido
18. Análisis Exploratorio y Reducción de la Dimensionalidad¶
18.1. Análisis de Componentes Principales¶
El análisis de componentes principales (PCA) es el proceso mediante el cual se calculan los componentes principales de una matriz de datos con el objeto de realizar una comprensión de los datos. PCA es un enfoque no supervisado, lo que significa que se realiza en un conjunto de variables \(X_1, X_2,…, X_d\) sin respuesta asociada \(Y\). PCA reduce la dimensionalidad del conjunto de datos, lo que permite explicar la mayor parte de la variabilidad utilizando menos variables. El PCA se usa comúnmente como una primera herramienta de visualización de los datos, para reducir el número de variables y evitar la multicolinealidad, o cuando se tienen demasiados predictores en relación con el número de observaciones.
18.1.1. Enfoque basado en proyecciones ortogonales¶
Sea \(X\) una matriz de \(n\) datos \(d\)-dimensionales, con cada componente de media nula, i.e.
Buscamos la dirección \(w'=(w_1,...,w_d)\) tal que la proyección de \(X\) sobre esta dirección maximice la varianza empírica de \(Xw\):
Tenemos que:
donde \(\hat{\Sigma}\) es la varianza empírica de \(X\):
Para maximizar la varianza \(\hat{\sigma}^2(Xw)\), construimos el Lagrangiano:
La condición de máximo queda:
Con lo cual \(w\) es un vector propio de \(\hat{\Sigma}\), y por lo tanto
la dirección de máxima varianza es la dirección asociada al vector propio cuyo valor propio es máximo. Este procedimiento puede iterarse para obtener la segunda proyección (ortogonal a la primera) de máxima varianza, que será el vector propio correspondiente al segundo mayor valor propio.
Referencias:
Kevin Murphy (2012) “Machine Learning, a probabilistic approach”, Capítulo 12. MIT Press
Hastie, Tibshirani and Friedman, “The elements of statistical learning” 2nd Ed., Springer, Capítulo 14
Ethem Alpayin (2004) “Introduction to Machine Learning”, Capítulo 6, MIT Press
suppressMessages(library("IRdisplay"))
display_png(file="figura1.png")

18.1.2. Enfoque de Descomposición en Valores Singulares (SVD)¶
Otro enfoque posible es considerar la descomposición siguiente para la matriz \(X\). Supongamos que \(n>d\), entonces existen matrices U, S, V tales que:
tales que \(U\) tiene columnas ortonormales, es decir \(U^TU = I_{dxd}\) y \(V\) con filas y columnas ortonormales, i.e., \(V^TV= VV^T= I_{dxd}\), y \(S\) es una matriz diagonal conteniendo los valores singulares \(\sigma_1,...,\sigma_d\).
Con esto, resulta que
donde \(D\) es la matriz diagonal que contiene los cuadrados de los valores singulares \({\sigma_1}^2,...,{\sigma_d}^2\). Y entonces:
Es decir \(V\) es la matriz de los vectores propios de \(\Sigma\) y \({\sigma_i}^2, i=1,...,d\) los valores propios respectivos.
Por otra parte:
con lo cual
Es decir \(U\) es la matriz de vectores propios de \(XX^T\) y \({\sigma_i}^2, i=1,...,d\) los valores propios respectivos.
Ejemplo Ilustrativo:
Consideremos el conjunto de datos de “USArrests” que está integrado en R. Este es un conjunto de datos que contiene cuatro variables que representan el número de arrestos por cada 100.000 residentes por asalto, asesinato y violación en cada uno de los cincuenta estados de EE. UU. en el año 1973. Los datos contienen también el porcentaje de la población que vive en áreas urbanas, UrbanPop.
data("USArrests")
head(USArrests, 10)
| Murder | Assault | UrbanPop | Rape | |
|---|---|---|---|---|
| <dbl> | <int> | <int> | <dbl> | |
| Alabama | 13.2 | 236 | 58 | 21.2 |
| Alaska | 10.0 | 263 | 48 | 44.5 |
| Arizona | 8.1 | 294 | 80 | 31.0 |
| Arkansas | 8.8 | 190 | 50 | 19.5 |
| California | 9.0 | 276 | 91 | 40.6 |
| Colorado | 7.9 | 204 | 78 | 38.7 |
| Connecticut | 3.3 | 110 | 77 | 11.1 |
| Delaware | 5.9 | 238 | 72 | 15.8 |
| Florida | 15.4 | 335 | 80 | 31.9 |
| Georgia | 17.4 | 211 | 60 | 25.8 |
Preparando los datos:
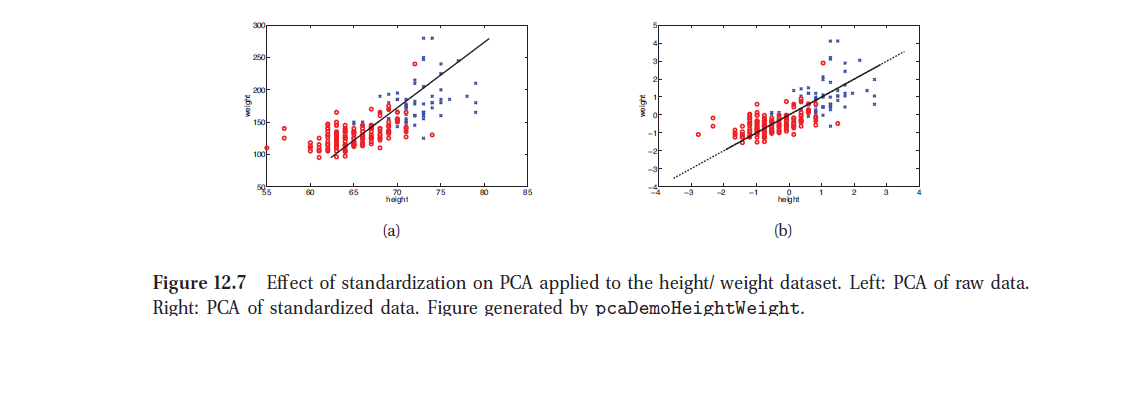
Para desarrollar los algoritmos vistos es preferible que cada variable se centre en cero y que tengan una escala común. Por ejemplo, la varianza de Asalto es 6945, mientras que la varianza de Asesinato es solo 18.97. Los datos de Asalto no son necesariamente más variables, simplemente están en una escala diferente en relación con el Asesinato.
display_png(file="figura2.png")
# calcula varianzas para cada variable
apply(USArrests, 2, var)
apply(USArrests,2,mean)
- Murder
- 18.9704653061224
- Assault
- 6945.16571428571
- UrbanPop
- 209.518775510204
- Rape
- 87.7291591836735
- Murder
- 7.788
- Assault
- 170.76
- UrbanPop
- 65.54
- Rape
- 21.232
Una posibilidad es estandarizar las variables:
# escalando los datos
scaled_df <- apply(USArrests, 2, scale)
head(scaled_df)
apply(scaled_df, 2, var)
apply(scaled_df, 2, mean)
| Murder | Assault | UrbanPop | Rape |
|---|---|---|---|
| 1.24256408 | 0.7828393 | -0.5209066 | -0.003416473 |
| 0.50786248 | 1.1068225 | -1.2117642 | 2.484202941 |
| 0.07163341 | 1.4788032 | 0.9989801 | 1.042878388 |
| 0.23234938 | 0.2308680 | -1.0735927 | -0.184916602 |
| 0.27826823 | 1.2628144 | 1.7589234 | 2.067820292 |
| 0.02571456 | 0.3988593 | 0.8608085 | 1.864967207 |
- Murder
- 1
- Assault
- 1
- UrbanPop
- 1
- Rape
- 1
- Murder
- -7.66308674501892e-17
- Assault
- 1.11240769200271e-16
- UrbanPop
- -4.33280798392555e-16
- Rape
- 8.94239109844319e-17
Sin embargo, no siempre el escalado deseable. Un ejemplo sería si cada variable en el conjunto de datos tuviera las mismas unidades y el analista deseara capturar esta diferencia en la varianza para sus resultados. Dado que Asesinato, Asalto y Violación se miden según las ocurrencias por cada 100,000 personas, esto puede ser razonable dependiendo de cómo quiera interpretar los resultados. Pero como UrbanPop se mide como un porcentaje de la población total, no tendría sentido comparar la variabilidad de UrbanPop con el asesinato, el asalto y la violación.
Lo importante a recordar es que el PCA está influenciado por la magnitud de cada variable; por lo tanto, los resultados obtenidos cuando realizamos PCA también dependerán de si las variables se han escalado individualmente.
El objetivo del PCA es explicar la mayor parte de la variabilidad en los datos con un número menor de variables que el conjunto de datos original. Para un conjunto de datos de gran tamaño con p variables, podríamos examinar las gráficas por pares de cada variable contra cada otra variable, pero incluso para un p moderado, el número de gráficos se vuelve excesivo y no es útil. Por ejemplo, cuando \(p = 10\) hay \(p (p − 1)/2 = 45\) diagramas de dispersión que podrían analizarse. Claramente, se requiere un método mejor para visualizar las n observaciones cuando p es grande. En particular, nos gustaría encontrar una representación de baja dimensión de los datos que capturen la mayor cantidad de información posible. Por ejemplo, si podemos obtener una representación bidimensional de los datos que capturan la mayor parte de la información, entonces podemos proyectar las observaciones en este espacio de baja dimensión.
PCA proporciona una herramienta para hacer precisamente esto. Encuentra una representación de baja dimensión de un conjunto de datos que contiene la mayor cantidad de variación posible. La idea es que cada una de las \(n\) observaciones vive en el espacio p-dimensional, pero no todas estas dimensiones son igualmente interesantes. PCA busca un pequeño número de dimensiones que sean lo más interesantes posible, donde el concepto de interesante se mide por la cantidad de observaciones que varían a lo largo de cada dimensión. Cada una de las dimensiones encontradas por PCA es una combinación lineal de las características p y podemos tomar estas combinaciones lineales de las mediciones y reducir el número de gráficos necesarios para el análisis visual mientras retenemos la mayor parte de la información presente en los datos.
# Calculando valores y vectores propios de la matriz de covarianzas empírica
arrests.cov <- cov(scaled_df)
arrests.eigen <- eigen(arrests.cov)
arrests.eigen
eigen() decomposition
$values
[1] 2.4802416 0.9897652 0.3565632 0.1734301
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.5358995 0.4181809 -0.3412327 0.64922780
[2,] -0.5831836 0.1879856 -0.2681484 -0.74340748
[3,] -0.2781909 -0.8728062 -0.3780158 0.13387773
[4,] -0.5434321 -0.1673186 0.8177779 0.08902432
# Extrayendo los pesos de los dos primeras componentes principales
w <- -arrests.eigen$vectors[,1:2]
row.names(w) <- c("Murder", "Assault", "UrbanPop", "Rape")
colnames(w) <- c("PC1", "PC2")
w
| PC1 | PC2 | |
|---|---|---|
| Murder | 0.5358995 | -0.4181809 |
| Assault | 0.5831836 | -0.1879856 |
| UrbanPop | 0.2781909 | 0.8728062 |
| Rape | 0.5434321 | 0.1673186 |
# Calcula proyección de los datos en cada componente principal
PC1 <- as.matrix(scaled_df) %*% w[,1]
PC2 <- as.matrix(scaled_df) %*% w[,2]
# Crea nuevo dataframe con la proyección
PC <- data.frame(State = row.names(USArrests), PC1, PC2)
head(PC)
| State | PC1 | PC2 | |
|---|---|---|---|
| <chr> | <dbl> | <dbl> | |
| 1 | Alabama | 0.9756604 | -1.1220012 |
| 2 | Alaska | 1.9305379 | -1.0624269 |
| 3 | Arizona | 1.7454429 | 0.7384595 |
| 4 | Arkansas | -0.1399989 | -1.1085423 |
| 5 | California | 2.4986128 | 1.5274267 |
| 6 | Colorado | 1.4993407 | 0.9776297 |
suppressMessages(library(tidyverse))
suppressMessages(library(ggplot2))
# Grafico en primer plano principal
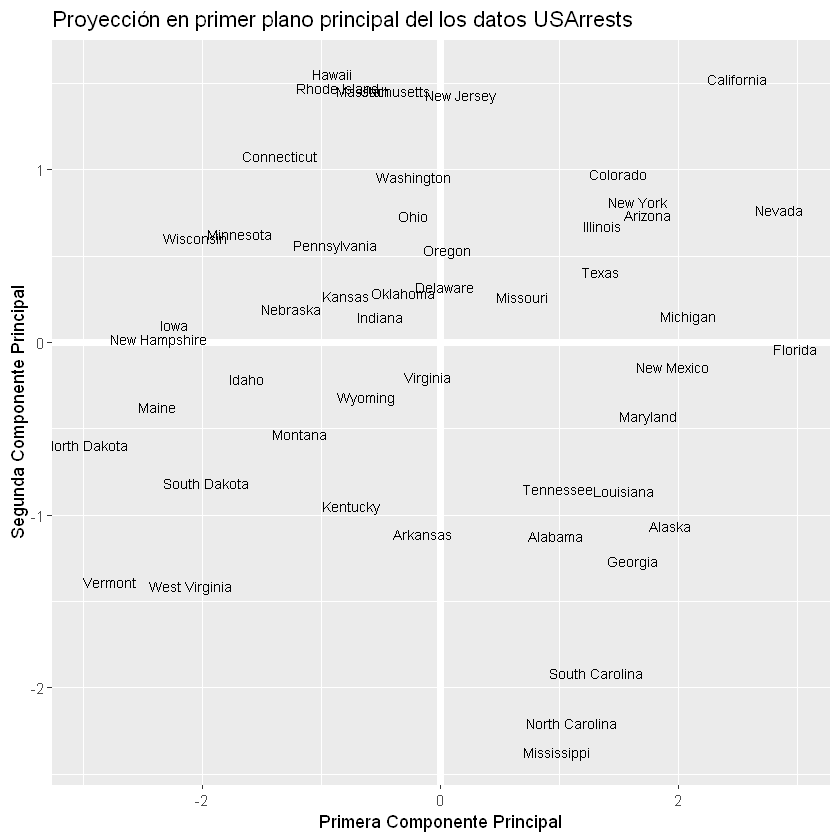
ggplot(PC, aes(PC1, PC2)) +
modelr::geom_ref_line(h = 0) +
modelr::geom_ref_line(v = 0) +
geom_text(aes(label = State), size = 3) +
xlab("Primera Componente Principal") +
ylab("Segunda Componente Principal") +
ggtitle("Proyección en primer plano principal del los datos USArrests")
18.1.3. Selección del número de componentes principales¶
Como ya se ha mencionado el PCA reduce la dimensionalidad al mismo tiempo que explica la mayor parte de la variabilidad, pero existe un método más técnico para medir exactamente qué porcentaje de la varianza se mantuvo en estos componentes principales.
La proporción de varianza explicada (PVE) por la m-ésima componente principal se calcula utilizando la ecuación:
De los cálculos previos se tiene que otra manera de calcular el PVE de la m-ésima componente principal es considerando los valores propios:
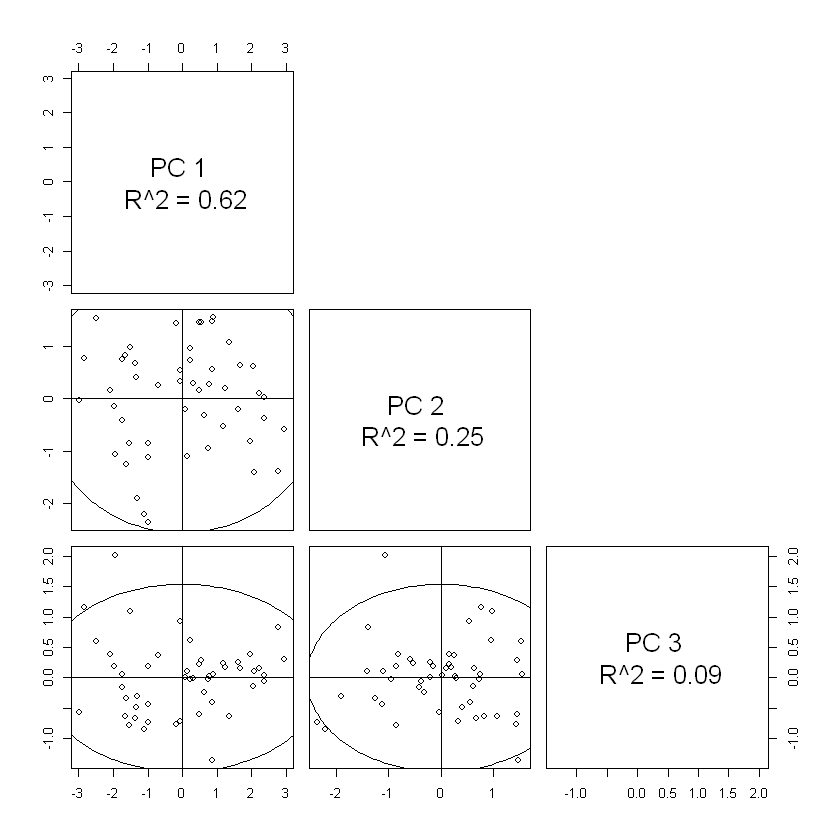
PVE <- arrests.eigen$values / sum(arrests.eigen$values)
round(PVE, 2)
- 0.62
- 0.25
- 0.09
- 0.04
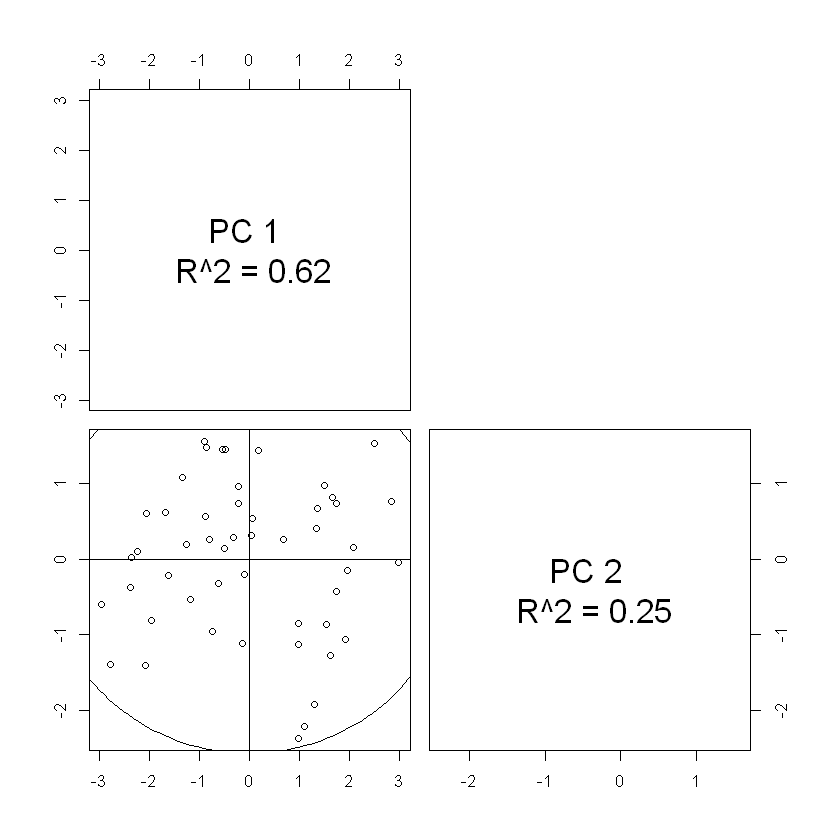
La primera componente principal en el ejemplo explica el 62% de la variabilidad, y la segunda componente principal explica el 25%. Juntas, las dos primeras componentes principales explican el 87% de la variabilidad.
# Gráfico de la PVE
par(mfrow=c(1,2))
PVEplot <- barplot(PVE,xlab="Componente Principal", ylab="PVE", main= "Gráfico PVE", ylim=c(0, 1), names.arg=c(1:4))
cumPVE <- barplot(cumsum(PVE),xlab="Componente Principal", ylab="", main= "Gráfico PVE Acumulada", names.arg=c(1:4))
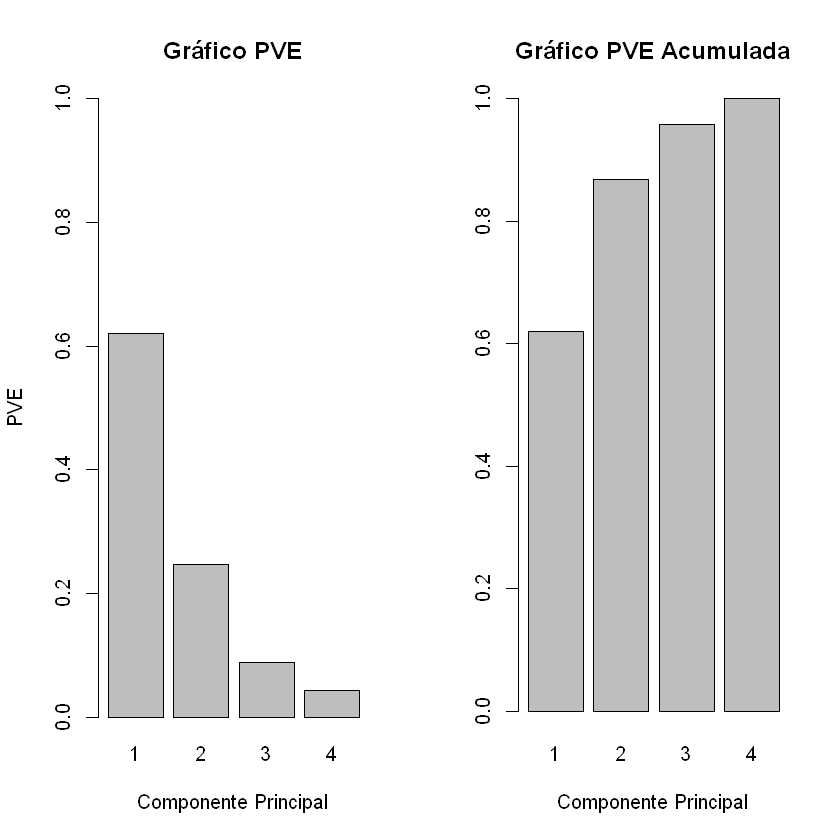
Número Óptimo de Componentes principales
En este ejemplo el número óptimo de componentes principales es 2, pues con ellas se conserva e 87% de la varianza.
Las funciones predefinidas en R:
datos <- as.matrix(USArrests)
pca_res <- prcomp(datos,scale=TRUE)
names(pca_res)
pca_res$sdev
pca_res$rotation <- -pca_res$rotation
pca_res$center
pca_res$scale
pca_res$x <- -pca_res$x
print(pca_res)
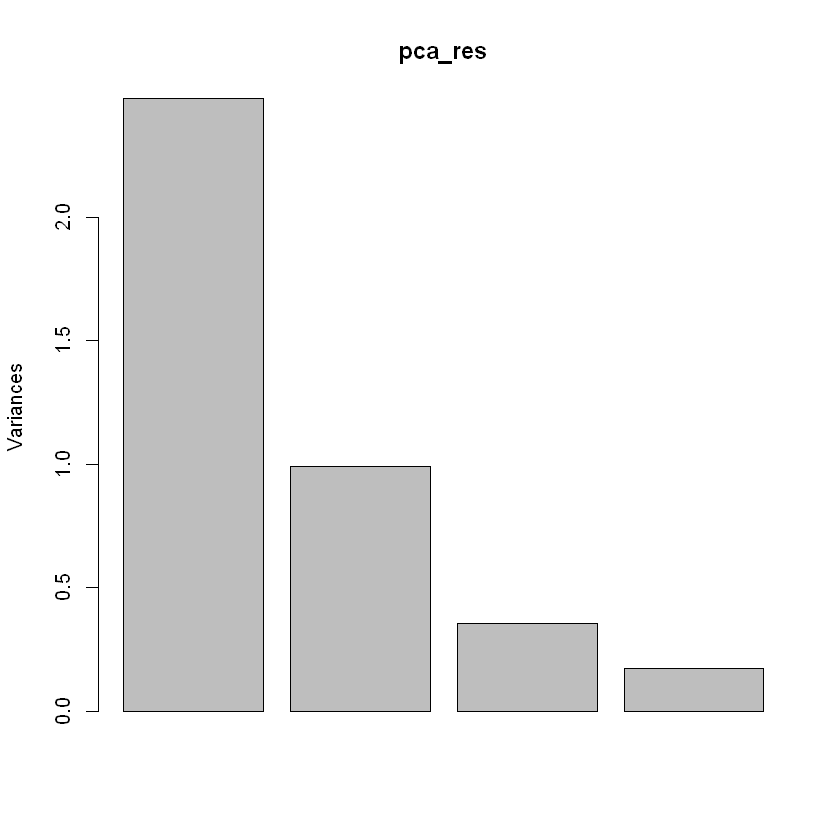
plot(pca_res)
barplot(cumsum(pca_res$sdev))
- 'sdev'
- 'rotation'
- 'center'
- 'scale'
- 'x'
- 1.57487827439123
- 0.994869414817764
- 0.597129115502527
- 0.41644938195396
- Murder
- 7.788
- Assault
- 170.76
- UrbanPop
- 65.54
- Rape
- 21.232
- Murder
- 4.35550976420929
- Assault
- 83.3376608400171
- UrbanPop
- 14.4747634008368
- Rape
- 9.36638453105965
Standard deviations (1, .., p=4):
[1] 1.5748783 0.9948694 0.5971291 0.4164494
Rotation (n x k) = (4 x 4):
PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432
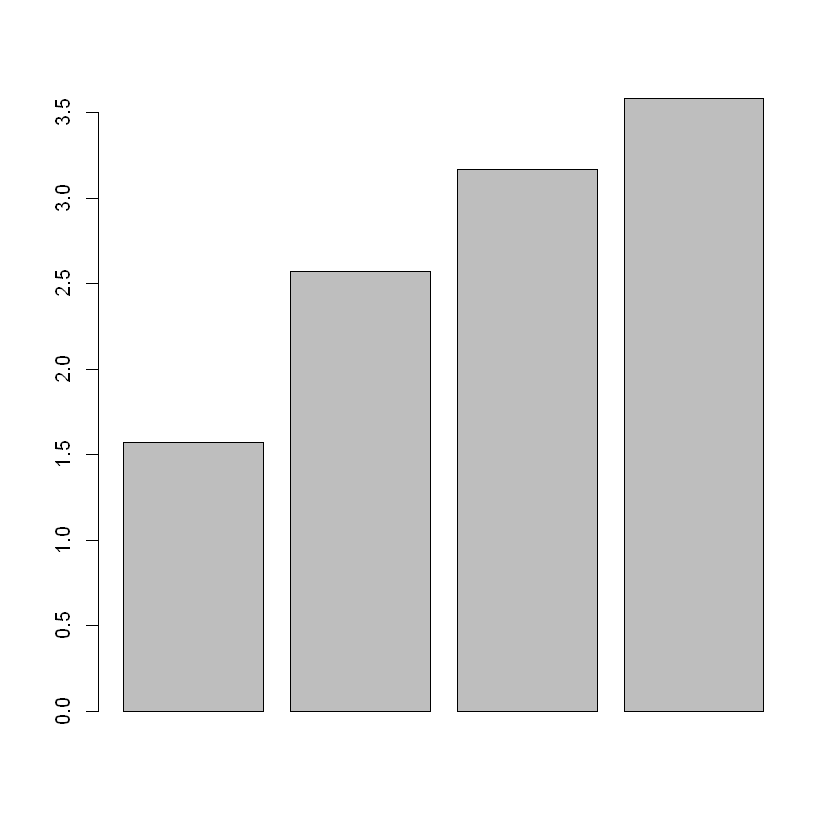
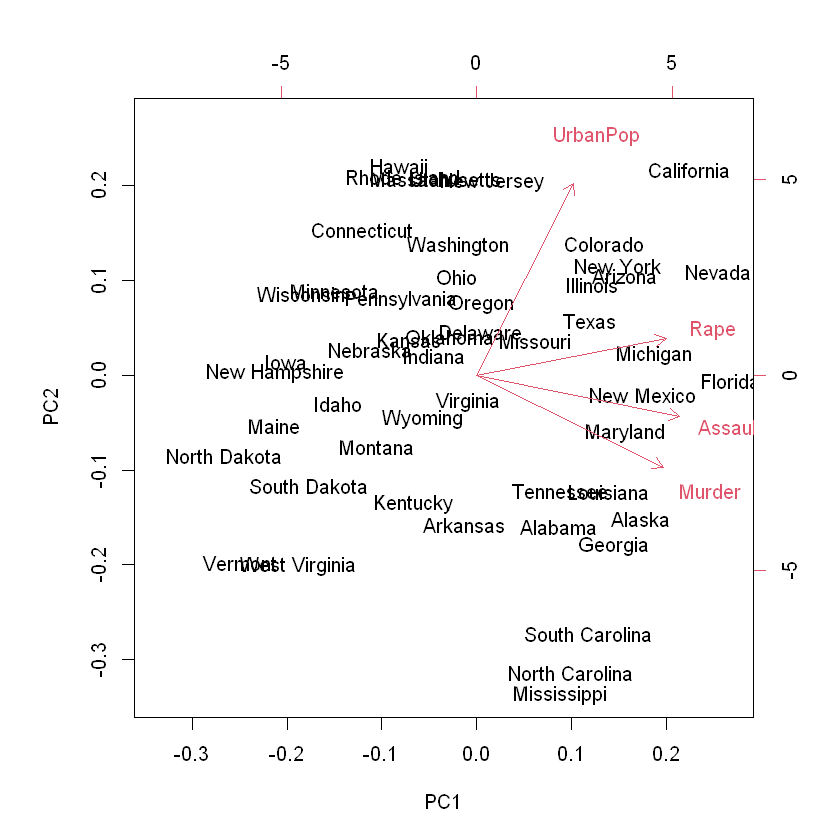
biplot(pca_res, scale = 0)

18.1.3.1. Ejercicio 2:¶
a) Explique a que corresponden cada una de las componente del objeto resultante de utilizar la función prcomp
b) Explique como se relacionan variables y observaciones en este último gráfico. Compare los resultados obtenidos utilizando la función predefinida en R prcomp con aquellos de los cálculos previos.
## recuperando los datos originales o una aproximación de ellos
print(datos)
pca_res <- prcomp(datos)
print(dim(datos))
#proyección en el primer plano principal
pr = pca_res$rotation[,1:4]
print(pr)
pr_datos <- datos%*%pr
print(pr_datos)
#volviendo al espacio original
rec <- pr_datos%*%t(pr)
print(rec)
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
Connecticut 3.3 110 77 11.1
Delaware 5.9 238 72 15.8
Florida 15.4 335 80 31.9
Georgia 17.4 211 60 25.8
Hawaii 5.3 46 83 20.2
Idaho 2.6 120 54 14.2
Illinois 10.4 249 83 24.0
Indiana 7.2 113 65 21.0
Iowa 2.2 56 57 11.3
Kansas 6.0 115 66 18.0
Kentucky 9.7 109 52 16.3
Louisiana 15.4 249 66 22.2
Maine 2.1 83 51 7.8
Maryland 11.3 300 67 27.8
Massachusetts 4.4 149 85 16.3
Michigan 12.1 255 74 35.1
Minnesota 2.7 72 66 14.9
Mississippi 16.1 259 44 17.1
Missouri 9.0 178 70 28.2
Montana 6.0 109 53 16.4
Nebraska 4.3 102 62 16.5
Nevada 12.2 252 81 46.0
New Hampshire 2.1 57 56 9.5
New Jersey 7.4 159 89 18.8
New Mexico 11.4 285 70 32.1
New York 11.1 254 86 26.1
North Carolina 13.0 337 45 16.1
North Dakota 0.8 45 44 7.3
Ohio 7.3 120 75 21.4
Oklahoma 6.6 151 68 20.0
Oregon 4.9 159 67 29.3
Pennsylvania 6.3 106 72 14.9
Rhode Island 3.4 174 87 8.3
South Carolina 14.4 279 48 22.5
South Dakota 3.8 86 45 12.8
Tennessee 13.2 188 59 26.9
Texas 12.7 201 80 25.5
Utah 3.2 120 80 22.9
Vermont 2.2 48 32 11.2
Virginia 8.5 156 63 20.7
Washington 4.0 145 73 26.2
West Virginia 5.7 81 39 9.3
Wisconsin 2.6 53 66 10.8
Wyoming 6.8 161 60 15.6
[1] 50 4
PC1 PC2 PC3 PC4
Murder 0.04170432 -0.04482166 0.07989066 -0.99492173
Assault 0.99522128 -0.05876003 -0.06756974 0.03893830
UrbanPop 0.04633575 0.97685748 -0.20054629 -0.05816914
Rape 0.07515550 0.20071807 0.97408059 0.07232502
PC1 PC2 PC3 PC4
Alabama 239.70349 46.45394 -5.8730769 -5.78404849
Alaska 267.72878 39.91901 16.7484308 0.71789947
Arizona 298.96954 66.73235 -5.0655924 0.97753765
Arkansas 193.24136 41.19804 -3.1679547 -2.85515395
California 282.32428 80.42202 3.3677289 -0.56432165
Colorado 209.87731 71.62154 8.9012188 -1.65468386
Connecticut 114.01404 70.83448 -11.7988012 -2.67624527
Delaware 241.63235 59.25575 -14.6591014 0.35183363
Florida 340.14570 64.17664 -6.3760772 -4.62382827
Georgia 215.43650 50.61171 0.2313854 -10.71982040
Hawaii 51.36522 82.19316 0.3462988 -6.84899696
Idaho 123.10432 48.43276 -4.8982076 -0.02831923
Illinois 253.89342 70.79901 -9.2614088 -3.74378830
Indiana 117.35036 60.74822 0.3600164 -5.02557772
Iowa 59.31454 54.55982 -4.0321734 -2.50665157
Kansas 119.11163 61.05919 -2.9937799 -4.02893925
Kentucky 112.51815 47.22868 -1.1410550 -7.25236397
Louisiana 253.17896 53.60703 -7.2060137 -7.85970656
Maine 85.64028 46.41412 -8.0705497 -1.25994807
Maryland 304.23146 52.89492 -5.7253169 -1.44782331
Massachusetts 153.63504 77.35213 -10.8852924 -2.34132861
Michigan 260.35285 63.80651 3.0861981 -3.87519545
Minnesota 75.94651 63.11155 -3.3715703 -2.64425189
Mississippi 261.75768 30.47353 -8.3815803 -7.25590524
Missouri 182.88761 63.17759 2.1224357 -4.05555306
Montana 112.41769 48.39145 -1.5397887 -3.62209021
Nebraska 105.80478 57.69076 -2.9101232 -2.71958113
Nevada 258.51490 73.00414 12.5105508 -3.71034380
New Hampshire 60.12397 53.16739 -5.6605310 -2.44023700
New Jersey 164.08560 81.03929 -9.6883014 -4.98857485
New Mexico 289.76949 57.56550 -1.1168741 -1.99489979
New York 259.19556 73.82592 -8.0994036 -4.26816691
North Carolina 339.22684 26.80534 -15.0743075 -1.26495482
North Dakota 47.40573 41.76691 -4.6899739 -1.07518364
Ohio 124.81450 70.18128 -1.7208133 -5.40526323
Oklahoma 155.20760 61.27208 -3.8312873 -3.19580182
Oregon 163.75109 61.76802 4.7518365 -0.46213667
Pennsylvania 110.21218 66.81350 -6.5846126 -5.25108287
Rhode Island 177.96530 76.27592 -20.8481637 -1.06788788
South Carolina 282.18239 34.36584 -5.4109391 -4.62789381
South Dakota 88.79461 41.30409 -2.0637641 -2.12386017
Tennessee 192.40759 51.39538 2.7219835 -7.29900331
Texas 206.19245 70.88691 -3.7715533 -7.61815161
Utah 124.98793 75.55041 -1.5899755 -1.50844232
Vermont 50.18686 30.58839 1.4246336 -1.37116188
Virginia 160.08388 56.14934 -2.3327559 -4.54998839
Washington 149.82549 67.86992 1.4029836 -0.68506570
West Virginia 83.35668 34.94907 -3.7801275 -4.11302566
Wisconsin 56.72500 63.40953 -6.0894648 -3.58111996
Wyoming 164.46679 51.97750 -7.1725909 -2.85828013
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
Connecticut 3.3 110 77 11.1
Delaware 5.9 238 72 15.8
Florida 15.4 335 80 31.9
Georgia 17.4 211 60 25.8
Hawaii 5.3 46 83 20.2
Idaho 2.6 120 54 14.2
Illinois 10.4 249 83 24.0
Indiana 7.2 113 65 21.0
Iowa 2.2 56 57 11.3
Kansas 6.0 115 66 18.0
Kentucky 9.7 109 52 16.3
Louisiana 15.4 249 66 22.2
Maine 2.1 83 51 7.8
Maryland 11.3 300 67 27.8
Massachusetts 4.4 149 85 16.3
Michigan 12.1 255 74 35.1
Minnesota 2.7 72 66 14.9
Mississippi 16.1 259 44 17.1
Missouri 9.0 178 70 28.2
Montana 6.0 109 53 16.4
Nebraska 4.3 102 62 16.5
Nevada 12.2 252 81 46.0
New Hampshire 2.1 57 56 9.5
New Jersey 7.4 159 89 18.8
New Mexico 11.4 285 70 32.1
New York 11.1 254 86 26.1
North Carolina 13.0 337 45 16.1
North Dakota 0.8 45 44 7.3
Ohio 7.3 120 75 21.4
Oklahoma 6.6 151 68 20.0
Oregon 4.9 159 67 29.3
Pennsylvania 6.3 106 72 14.9
Rhode Island 3.4 174 87 8.3
South Carolina 14.4 279 48 22.5
South Dakota 3.8 86 45 12.8
Tennessee 13.2 188 59 26.9
Texas 12.7 201 80 25.5
Utah 3.2 120 80 22.9
Vermont 2.2 48 32 11.2
Virginia 8.5 156 63 20.7
Washington 4.0 145 73 26.2
West Virginia 5.7 81 39 9.3
Wisconsin 2.6 53 66 10.8
Wyoming 6.8 161 60 15.6
Volviendo al ejemplo de los dígitos:
mnist <- read.csv("mnist_train.csv",header=FALSE)
#agregando nombres a las columnas
colnames(mnist)[1]<-"Digit"
for(i in seq(2,ncol(mnist),by=1)){colnames(mnist)[i]<-paste("pixel",as.character(i-1),sep = "")}
#selección de datos que representan el Nro 3
datos3 <- mnist[mnist$Digit==3,-1]
print(dim(datos3))
[1] 1431 784
##separando las columnas con sólo 0`s
datos <- matrix(0,nrow=1431,ncol=784)
col0 <- 0
k=0
for (j in 1:784){
vec <- as.numeric(datos3[,j])
if(sum(vec)==0)
col0 <-c(col0,j)
else{
k <- k+1
datos[,k] <- vec
}
}
datos <- datos[,1:k]
col0 <- col0[-1]
print(dim(datos))
print(length(col0))
[1] 1431 536
[1] 248
#reducción de dimensiones usando PCA
res <- prcomp(datos)
#utilizando j componentes
j=10
pr = matrix(res$rotation[,1:j],ncol=j,nrow=536)
#proyección en j componentes
pr_datos <- datos%*%pr
#reconstrucción a partir de la proyección en j componentes
rec <- trunc(pr_datos%*%t(pr))
rect <- rec
#truncando al rango de valores de grises
rect[rec[,]<0]<-0
rect[rec[,]>255]<-255
#agregando las columnas con ceros
datosR <- matrix(0,ncol=784,nrow=1431)
k<-1
l<-1
for (j in 1:784){
if (j!=col0[k]){
datosR[,j]<-rect[,l]
l<-l+1
}
else
k <- k+1
}
#comparación de la representación de una observación considerando las 784 variables o j
digit <- matrix(as.numeric(datos3[48,]), nrow = 28)
image(digit, col = grey.colors(255))
digitR <- matrix(as.numeric(datosR[48,]),nrow=28)
image(digitR, col = grey.colors(255))
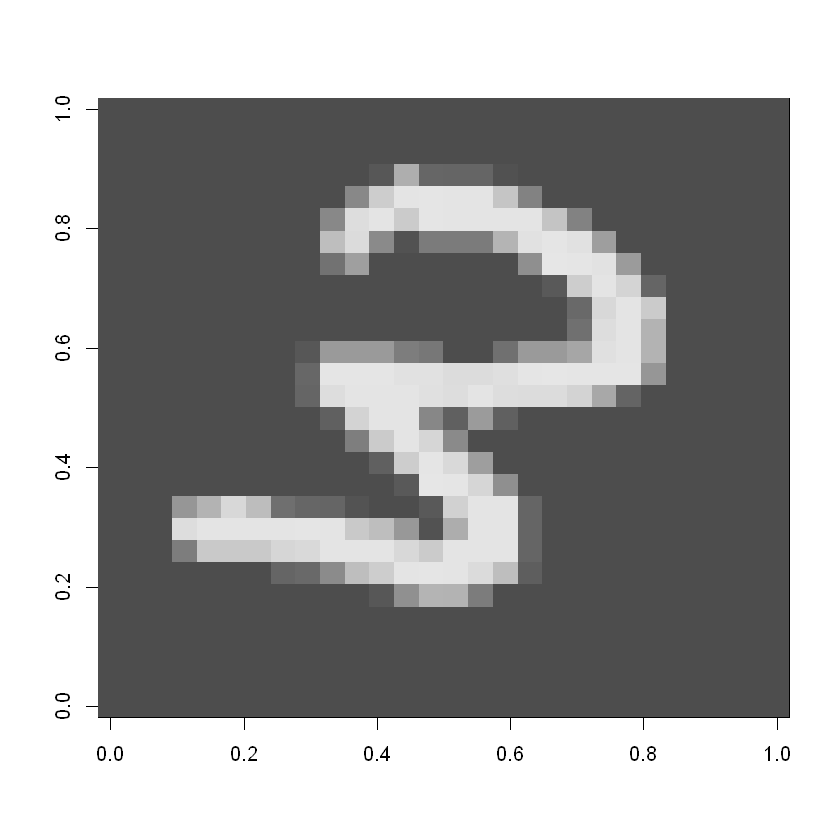
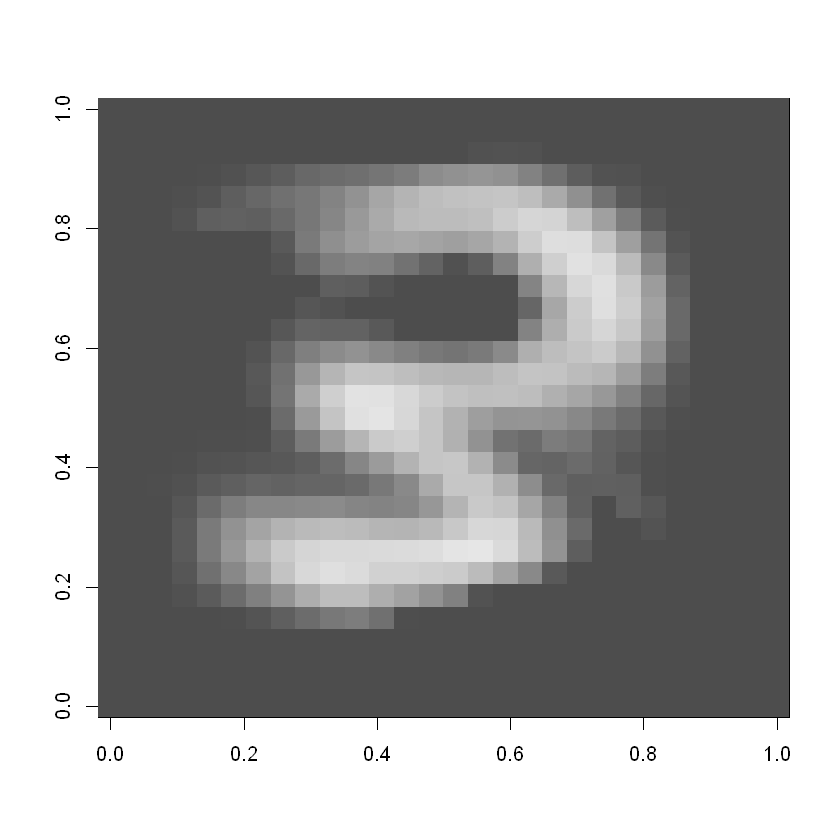
18.2. Otro enfoque: Modelos Lineales Latentes¶
18.2.1. Análisis Factorial¶
Consideremos que asociado a un vector aleatorio \(d\)-dimensional \(x_i\) existe un vector aleatorio de variables latentes \(z_i\) de menor dimension, \(l\), que cumple:
y
donde \(W\) matriz de dimensiones \(dxl\) es conocida como matriz de coeficientes factoriales y \(\Psi\) es la matriz de covarianza de dimensión \(dxd\)
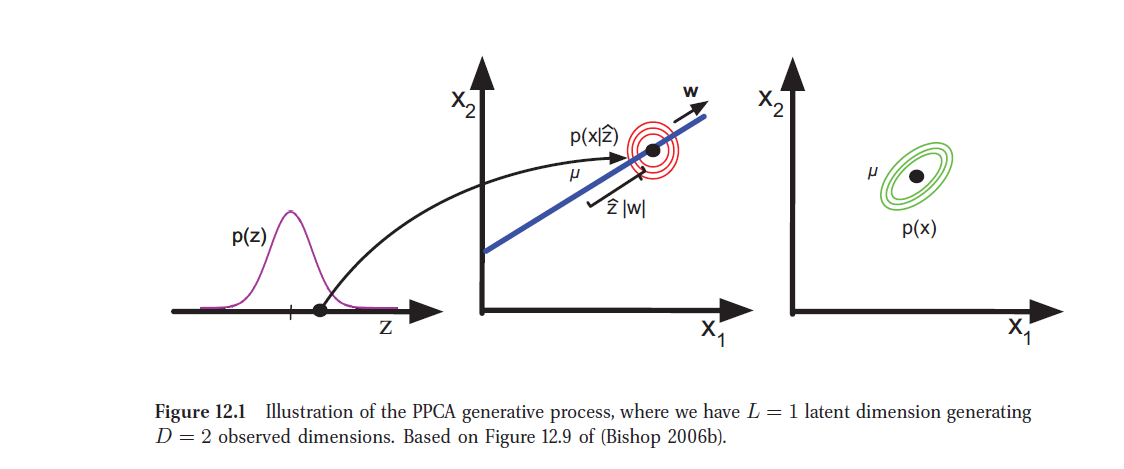
La idea principal del Análisis Factorial es que \(\Psi\) es una matriz diagonal, es decir, que toda la correlación de las variables originales se concentra en las variables latentes. El caso especial en que:
se denomina Análisis de Componentes Principales Probabilístico (PPCA).
display_png(file="figura3.png")
En este contexto, si agregamos como restricciones que \(W\) sea ortonormal y que \(\sigma^2 \to 0\), el modelo se reduce al PCA clásico.
En efecto, se puede formular el siguiente teorema:
Teorema 1: Supongamos que buscamos una base lineal ortogonal de \(l\) vectores \(w_j \in \mathbb{R}^d\) y las correspondientes variables latentes \(z_i \in \mathbb{R}^l\), tales que se minimice el error de reconstrucción medio:
donde
Entonces, sujeto a que \(W\) es ortonormal, se puede demostrar que la solución óptima es
donde \(V_l\) contiene los \(l\) vectores propios asociados a los mayores valores propios de la matrix de covarianzas empìricas de \(X\):
Además la codificación óptima de los datos de dimensión \(l\) es
que es la proyección de los datos en el espacio generado por los primeros \(l\) vectores propios de \(\Sigma\).
Demostración: ver en Murphy “Machine Learning, a probabilistic approach”, Capítulo 12.
En el caso general \(\sigma^2 >0\) se tiene el siguiente teorema, que corresponde al PPCA.
Teorema 2: Considere el modelo de análisis factorial con \(\Psi = \sigma^2 I\). Entonces, se cumple que el log de la verosimilitud observada es: $\(log p(X \mid W, \sigma^2) = \frac{-n}{2} ln |C| - \frac{1}{2}\sum_{i=1}^n {x_i}^T C^{-1} x_i = \frac{-n}{2} ln |C| + tr(C^{-1} \hat{\Sigma})\)\( donde \)\(C = WW^T + \sigma^2 I\)\( y \)\(\hat{\Sigma} = \frac{1}{n} \sum_{i=1}^n x_i^T {x_i}\)\( Se puede mostrar que este caso, los estimadores de máxima verosimilitud de \)W\( y \)\sigma^2$ están dados por:
donde \(V\) es la matriz cuyas columnas son los \(l\) primeros vectores propios de \(\hat{\Sigma}\) y \(\Lambda\) es una matriz diagonal de \(lxl\) de los valores propios correspondientes. Además, $\(\hat{\sigma}^2 = \frac{1}{d-l} \sum_{j=l+1}^d \lambda_j\)$ que es la varianza promedio asociada a las dimensiones descartadas.
Demostración: Tipping y Bishop, 1999 (ver en Murphy “Machine Learning, a probabilistic approach”, Capítulo 12.)
display_png(file="figura4.png")
##if (!requireNamespace("BiocManager", quietly = TRUE))
## install.packages("BiocManager")
##
##BiocManager::install("pcaMethods")
suppressMessages(library("pcaMethods"))
datos <- as.matrix(USArrests)
datos <- scale(datos)
result <- pca(datos, method="ppca", nPcs=3, seed=123)
## Get the estimated complete observations
cObs <- completeObs(result)
## Plot the scores
plotPcs(result, type = "scores")
result <- pca(datos, method="ppca", nPcs=2, seed=123)
## Get the estimated complete observations
cObs <- completeObs(result)
## Plot the scores
plotPcs(result, type = "scores")
biplot(result)