16. Regresión lineal con funciones base y Regularización¶

16.1. Modelo general de regresión lineal¶

Anteriormente aprendimos como ajustar lineas e hiperplanos a datos continuos. Sin embargo, la forma más general de un modelo lineal es:

\[ g_\theta(x_i) = \sum_{k=0}^K \theta_k \phi_k(x_i), \]

donde \(\phi_k: \mathbb{R}^D \to \mathbb{R}\) es una transformación que pueder no-lineal. Notemos además que \(K\) y \(D\) no necesariamente están relacionados. A continuación veremos algunos ejemplos.

Base Polinomial: Para una variable unidimensional \(x_i \in \mathbb{R}, i=1,\ldots,N\) se puede definir una base polinomial como:

\[ \phi_k(x_i) = x_i^k \]

que resulta en un model polinomial de grado \(K\):

\[ g_\theta(x_i) = \sum_{k=0}^K \theta_k x_i^k = \theta_0 + \theta_1 x_i + \theta_2 x_i^2 + \ldots + \theta_K x_i^K \quad \forall i \]

Base Trigonométrica: Si queremos modelar un comportamiento periódico en la variable independiente una buena opción es utilizar una base trigonométrica, e.g. una serie de Fourier.

Para una variable unidimensional \(x_i \in \mathbb{R}, i=1,\ldots,N\), una base trigonométrica con periodo \(P=1/f_0\) sería:

\[\begin{split} \phi_k(x_i) = \begin{cases} 1 & k=0 \\ \cos(2\pi k f_0 x_i) & k \in [1, K] \\ \sin(2\pi k f_0 x_i) & k \in [K+1, 2K] \end{cases} \end{split}\]

que resulta en un modelo con \(2K+1\) parámetros:

\[ g_\theta(x_i) = \theta_0 + \sum_{k=1}^K \theta_k \cos(2\pi k f_0 x_i) + \sum_{k=1}^K \theta_{k+K} \sin(2\pi k f_0 x_i) \]

Modelar interacciones entre variables: Podemos crear una base que modela interacciones no lineales entre las variables independientes.

Por ejemplo, si tienemos una variable independiente bidimensional (dos columnas) \(x_i = (w_{i}, v_{i}), i=1,\ldots,N\) un modelo con interacciones hasta de segundo orden sería:

\[ g_\theta(x_i) = \theta_0 + \theta_1 w_i + \theta_2 v_i + \theta_3 w_i^2 + \theta_4 v_i w_i + + \theta_5 v_i^2 \]

16.2. Regresión polinomial con `statsmodels`¶

Podemos hacer una regresión lineal con funciones base utilizando el método from_formula de OLS. Este método recibe una formula como string y un DataFrame de Pandas con los datos.

Por ejemplo, si nuestro DataFrame tiene columnas llamadas Y y X, y queremos ajustar un modelo que prediga Y en función de X, la fórmula sería: Y ~ X.

Ver también

La fórmula anterior está escrita en un “mini-lenguaje” implementado por la librería patsy. Este lenguaje para definir modelos estadísticos está inspirado en R. Revise la documentación si tiene interés en definir modelos más avanzados que los que se verán a continuación.

Veamos el siguiente dataset sintético:

np.random.seed(1234)
x = np.random.randn(30)
y = -0.5*x**4 + 2*x**3 -3 + np.random.randn(len(x))
df = pd.DataFrame({'X': x, 'Y': y})

Así se utilizaría from_formula para crear un modelo que prediga la variable Y dado X

result = sm.OLS.from_formula(formula='Y ~ X', data=df).fit()
result.params

Intercept   -5.445831
X            6.764197
dtype: float64

Nota

Por defecto, statsmodels agrega un parámetro de intercepta en el modelo lineal

Luego podemos hacer una predicción con:

hatX = pd.DataFrame({'X': np.linspace(-3, 3, num=100)})
hatY = result.predict(hatX)

hv.Overlay([hv.Curve((hatX, hatY), 'X', 'Y', label='model'), 
            hv.Scatter((x, y), label='data').opts(color='k')]).opts(legend_position='top_left')

Podemos extender el modelo anterior agregamos más términos a la fórmula. Por ejemplo podríamos agregar términos cuadráticos y cúbicos con:

result = sm.OLS.from_formula(formula='Y ~ X + I(X ** 2) + I(X ** 3)', data=df).fit()

display(result.params)

hatY = result.predict(hatX)

Intercept   -2.731240
X           -0.602724
I(X ** 2)   -1.039263
I(X ** 3)    2.659100
dtype: float64

hv.Overlay([hv.Curve((hatX, hatY), 'X', 'Y', label='model'), 
            hv.Scatter((x, y), label='data').opts(color='k')]).opts(legend_position='top_left')

¿Qué ocurre si aumentamos el grado del polinomio arbitrariamente?

hatY = {}
for k in range(1, 16):
    many_terms = "".join([f'+ I(X ** {j})' for j in range(2, k+1)])
    result = sm.OLS.from_formula(formula='Y ~ X'+many_terms, data=df).fit()
    hatY[k] = result.predict(hatX)

hMap = hv.HoloMap(kdims=['degree'])
for degree, haty_ in hatY.items():
    p_model = hv.Curve((hatX, haty_), 'X', 'Y', label='model')
    p_data = hv.Scatter((x, y), label='data').opts(color='k')
    hMap[degree] = hv.Overlay([p_model, p_data]).opts(legend_position='top_left', ylim=(-40., 20.))

hMap            

Peligro

A medida que el grado del polinomio crece, el modelo se sobreajusta los datos cada vez más.

A continuación definiremos el concepto de sobreajuste y luego veremos como evitarlo utilizando regularización.

16.3. Sobreajuste y regularización¶

En el ejemplo anterior, el grado del modelo polinomial representa la complejidad del modelo. En general mientras más complejo es un modelo, mayor es su flexibilidad para acomodarse a los datos.

Pero demasiada complejidad puede devenir en sobreajuste

Sobreajuste se refiere cuando ajustamos los datos con un error cercano a cero.

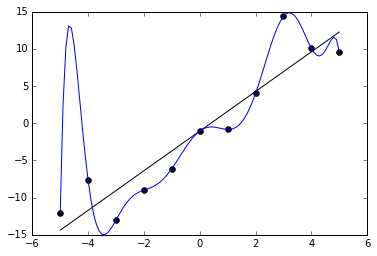
https://upload.wikimedia.org/wikipedia/commons/6/68/Overfitted_Data.png

Lo anterior es perjudicial pues, en general estaríamos ajustando el ruido en los datos y perdiendo capacidad de generalizar a datos nuevos.

Para evitar sobreajuste podemos

Usar modelos de baja complejidad
Decidir la complejidad utilizando técnicas de validación cruzada
Penalizar la complejidad mediante regularización

Ver también

Para una tratamiento más extenso sobre sobreajuste y estrategias de validación cruzada recomiendo revisar el siguiente material

16.3.1. Compromiso sesgo-varianza¶

Asumamos que nuestros datos pueden modelarse con una función suave y ruido aditivo gaussiano:

\[ y = f(x) + \varepsilon \]

y que ajustaremos los datos con un modelo lineal. Podemos medir la calidad del ajuste en base al error cuadrático medio (mean square error, MSE), que puede descomponerse como sigue:

\[ \mathbb{E}[(y - \hat y)^2] = \sigma^2 + (f - \mathbb{E}[\hat y])^2 + \text{Var}[\hat y], \]

donde

el primer término está asociado al error irreducible (ruido de los datos)
el segundo término es el cuadrado del sesgo del estimador
el tercer término es la varianza del estimador

De la descomposición es fácil ver que el MSE puede ser pequeño si el sesgo es pequeño o si la varianza es pequeña.

Los modelos simples suelen tener alto sesgo y baja varianza
Los modelos complejos suelen tener bajo sesgo y alta varianza

El teorema de Gauss-Markov dice que OLS es el estimador insesgado de mínima varianza. Pero los modelos con sesgo cero no son necesariamente buenos si la complejidad es alta (sobreajuste).

Importante

Si estamos en un régimen sobreajustado, puede ser interesante disminuir la varianza a costa de aumentar un poco el sesgo. Esto se puede lograr penalizando la complejidad.

16.3.2. Mínimos cuadrados penalizado o Ridge Regression¶

Si asumimos una verosimilitud Gaussiana y un prior Gaussiano podemos escribir el logaritmo de la distribución conjunta:

\[\begin{split} \begin{split} \log p({x}, \theta) &= \log \prod_{i=1}^N \mathcal{N}(y_i | f_\theta(x_i), \sigma^2) + \log \prod_{j=1}^M \mathcal{N}(\theta_j | 0, \sigma_0^2) \\ &= -\frac{N}{2} \log(2\pi \sigma^2) - \frac{1}{2\sigma^2} (Y-X\theta)^T (Y - X\theta) -\frac{M}{2} \log(2\pi \sigma_0^2) - \frac{1}{2\sigma_0^2} \|\theta\|^2 \end{split} \end{split}\]

En este caso, el estimador MAP de \(\theta\) está dado por:

\[\begin{split} \begin{split} \hat \theta &= \text{arg}\max_\theta \log p({x}, \theta) \\ &= \text{arg}\max_\theta - \frac{1}{2\sigma^2} (Y-X\theta)^T (Y - X\theta) - \frac{1}{2\sigma_0^2} \|\theta\|^2 \\ &= \text{arg}\min_\theta (Y-X\theta)^T (Y - X\theta) + \alpha \|\theta\|^2 \end{split} \end{split}\]

donde \(\alpha = \frac{\sigma^2}{\sigma_0^2}\)

Cuya solución se obtiene derivado en función de \(\theta\) e igualando a cero:

\[ \frac{d}{d\theta} (Y-X\theta)^T (Y - X\theta) + \lambda \|\theta\|^2 = -X^T (Y - X\theta) + \alpha \theta = 0 \]

y finalmente:

\[ \hat \theta = (X^T X + \alpha I)^{-1} X^T Y \]

que se conoce como la solución de mínimos cuadrados regularizado, ridge regression o regularización de Tikhonov.

Nota

El prior Gaussiano es equivalente a implementar una penalización con norma \(L_2\) de \(\theta\). Distintos priors dan a lugar distintas penalizaciones, por ejemplo un prior Laplaciano resulta en una penalización con norma \(L_1\).

Importante

Regularizar un modelo consiste en añadir un término penalizador o restricción a la función de costo a minimizar, con tal de evitar sobreajuste o problemas numéricos relacionados a problemas “mal puestos” (ill-posed).

En el caso de los mínimos cuadrados regularizados, el hiperparámetro \(\alpha\) controla el compromiso entre minimizar el error cuadrático y minimizar la norma de los parámetros.

Si \(\alpha\) es muy pequeño es como ignorar la penalización (se reduce a OLS)
Si \(\alpha\) es muy grande entonces se puede inducir una penalización excesiva, donde el modelo no es capaz de ajustarse a los datos

Podemos seleccionar \(\alpha\) utilizando validación cruzada o el método de la “curva L”, el cual consiste en encontrar el codo de la curva de \( \log (Y-X\theta)^T (Y - X\theta)\) vs \( \log \|\theta\|^2\).

16.4. Mínimos cuadrados regularizados con `statsmodels`¶

Podemos ajustar un modelo de mínimos cuadrados regularizados utilizando la función fit_regularized de OLS. En particular, si utilizamos el argumento L1_wt=0 entonces estaremos haciendo regresión ridge. Si utilizamos L1_wt=1 estaremos haciendo regularización con norma \(L_1\) (que se conoce como LASSO).

Veamos como cambia el resultado de mínimos cuadrados regularizados en función de \(\alpha\) para un polinomio de grado 15

many_terms = "".join([f'+ I(X ** {j})' for j in range(2, 16)])
hatY = {}
for alpha in [0, 1e-4, 1e-2, 1., 1e+2, 1e+4, 1e+10]:
    result = sm.OLS.from_formula(formula='Y ~ X'+many_terms, data=df).fit_regularized(L1_wt=0, alpha=alpha)
    hatY[alpha] = result.predict(hatX)

hMap = hv.HoloMap(kdims=['alpha'])
for alpha, haty_ in hatY.items():
    p_model = hv.Curve((hatX, haty_), 'X', 'Y', label='model')
    p_data = hv.Scatter((x, y), label='data').opts(color='k')
    hMap[alpha] = hv.Overlay([p_model, p_data]).opts(legend_position='top_left', ylim=(-40.0, 20.0))

hMap            

Observaciones

Aplicar regularización puede disminuir el sobreajuste en modelos complejos
Pero, si la penalización es excesiva, se puede llegar a una solución trivial (linea horizontal)

Herramientas estadísticas para la investigación

Regresión lineal con funciones base y Regularización

Contenido

16. Regresión lineal con funciones base y Regularización¶

16.1. Modelo general de regresión lineal¶

16.2. Regresión polinomial con `statsmodels`¶

16.3. Sobreajuste y regularización¶

16.3.1. Compromiso sesgo-varianza¶

16.3.2. Mínimos cuadrados penalizado o Ridge Regression¶

16.4. Mínimos cuadrados regularizados con `statsmodels`¶

Herramientas estadísticas para la investigación

Regresión lineal con funciones base y Regularización

Contenido

16. Regresión lineal con funciones base y Regularización¶

16.1. Modelo general de regresión lineal¶

16.2. Regresión polinomial con statsmodels¶

16.3. Sobreajuste y regularización¶

16.3.1. Compromiso sesgo-varianza¶

16.3.2. Mínimos cuadrados penalizado o Ridge Regression¶

16.4. Mínimos cuadrados regularizados con statsmodels¶

16.2. Regresión polinomial con `statsmodels`¶

16.4. Mínimos cuadrados regularizados con `statsmodels`¶