Variables Aleatorias
Contenido
2. Variables Aleatorias¶
Variables aleatorias
Probabilidades puntuales, funciones de densidad y funciones de distribución acumuladas.
Una variable aleatoria es una función que asigna un número a cada elemento en el espacio muestral de un experimento aleatorio. Se denomina Variable Aleatoria Discreta si los valores son enteros:
\(\begin{array}{cc} X:& \Omega \to \mathbb{N}\\ &\omega \to X(\omega) \end{array}\)
y Variable Aleatoria Continua si los valores son reales:
\(\begin{array}{cc} X:& \Omega \to \mathbb{R}\\ &\omega \to X(\omega) \end{array}\)
Ejemplos:
\(\begin{array}{ll} X:& \Omega \to \{0,1\}\\ &\omega \to X(\omega)= \left\{\begin{array}{ll} 1 & \omega=cara\\ 0 & \omega=sello \\ \end{array} \right .\\ &\\ X:& \Omega \to [0,\infty) \\ &\omega \to X(\omega)= t \\ \end{array}\)
donde \(t\) es el tiempo de falla de una máquina y \(\omega\) es el evento de falla con todas sus características no necesariamente observables.
2.1. Función de probabilidad puntual¶
En el caso de variables aleatorias discretas, la probabilidades se definen mediante una función de probabilidad puntual.
Ejemplo:
\(\begin{array}{ll} X:& \Omega \to \mathbb{N}\\ &\omega \to X(\omega)= n \\ \end{array}\)
dónde n representa el número de clientes que llegan al banco el lunes entre 9 y 10 am
##caso en que el nro de clientes se modela como Poisson de media 10
library(rbokeh)
vec <- seq(0,30,1)
pvec <- dpois(vec,10)
p <- figure(plot_width=600,plot_height=300, title="Ejemplo probabilidad puntual Poisson", title_location="above") %>%
ly_points(vec,pvec, hover = list(vec,pvec))%>%
ly_segments(vec,rep(0,30),vec,pvec)
p
2.2. Función de densidad de probabilidad¶
En el caso de variables aleatorias continuas, las probabilidades se definen mediante una función de densidad de probabilidad:
\(\begin{array}{ll} f_X:& \mathbb{R} \to \mathbb{R_+}\\ &x \to f_X(x) \\ \end{array}\)
Ejemplo:
\(\begin{array}{ll} X:& \Omega \to \mathbb{R}\\ &\omega \to X(\omega)= x \\ f_X(x)& = \frac{1}{2\sqrt{2\pi}} exp(\frac{-(x-60)^2}{8}) \end{array}\)
dónde x representa el peso de un individuo.
library(rbokeh)
vec <- seq(50,70,by=0.1)
vec2 <- seq(58,62,by=0.1)
pvec <- dnorm(vec,60,2)
par(cex=0.8)
p <- figure(plot_width=600,plot_height=300, title="Ejemplo densidad Normal", title_location="above") %>%
ly_lines(vec,pvec) %>%
ly_abline( h=0) %>%
ly_polygons( x = c(58,vec2,62), y =c(0,dnorm(vec2,60,2),0), col = "grey")
p
prob = pnorm(62,60,2)-pnorm(58,60,2)
print(prob)
[1] 0.6826895
2.3. Función de distribución de probabilidad acumulada¶
Es la función \(F_X\) que devuelve la probabilidad de que una v.a. sea menor o igual que un valor.
En el caso de las v.a. discretas se calcula como:
\(\begin{array}{ll} P(X \leq x) = F_X(x) & = \sum_{t=1}^x \limits P(X = t) \end{array}\)
En el caso de las v.a. continuas se calcula como:
\(\begin{array}{llll} P(X \leq x) = &F_X(x)& = &\int_{-\infty}^x f(x)dx\\ &f_X(x)& = & \frac{d}{dx} F_X(x) \end{array}\)
Y una manera alternativa de obtener la probabilidad:
\(\begin{array}{l} P(a \leq X \leq b) = F_X(b) - F_X(a)\\ \end{array}\)
library(rbokeh)
##distribución Poisson acumulada
vec <- seq(1,30,by=1)
pvec <- ppois(vec,10)
p1 <- figure(plot_width=600,plot_height=200, title="Prob. Acumulada: Caso Discreto", title_location="above") %>%
ly_points(vec,pvec, hover = list(vec,pvec))%>%
ly_segments(vec,rep(0,30),vec,pvec)
p1
##distribución normal acumulada
vec <- seq(40,80,by=0.1)
pvec1 <- pnorm(vec,60,2)
pvec2 <- pnorm(vec,60,8)
pvec3 <- pnorm(vec,60,4)
p2 <- figure(plot_width=600,plot_height=200, title="Prob. Acumulada: Caso Continuo", title_location="above", legend_location = "bottom_right") %>%
ly_lines(vec,pvec1,legend="sd=2") %>%
ly_lines(vec,pvec2,col="blue",legend="sd=8") %>%
ly_lines(vec,pvec3,col="red",legend="sd=4")
p2
2.4. Variables Aleatorias Multidimensionales¶
Se trata de funciones que asignan un vector multidimensional al resultado de un experimento aleatorio. Se denomina Vector Aleatorio Discreto si los valores son enteros multidimensionales:
\(\begin{array}{cl} {\bf X}:& \Omega \to \mathbb N^k\\ &\omega \to {\bf X}(\omega)=(X_1(\omega),\cdots,X_k(\omega)) = (n_1,\cdots,n_k) \end{array}\)
y Vector Aleatorio Continuo si los valores son reales multidimensionales:
\(\begin{array}{cl} {\bf X}:& \Omega \to \mathbb R^k\\ &\omega \to {\bf X}(\omega)=(X_1(\omega),\cdots,X_k(\omega)) = (x_1,\cdots,x_k) \end{array}\)
Ejemplo:
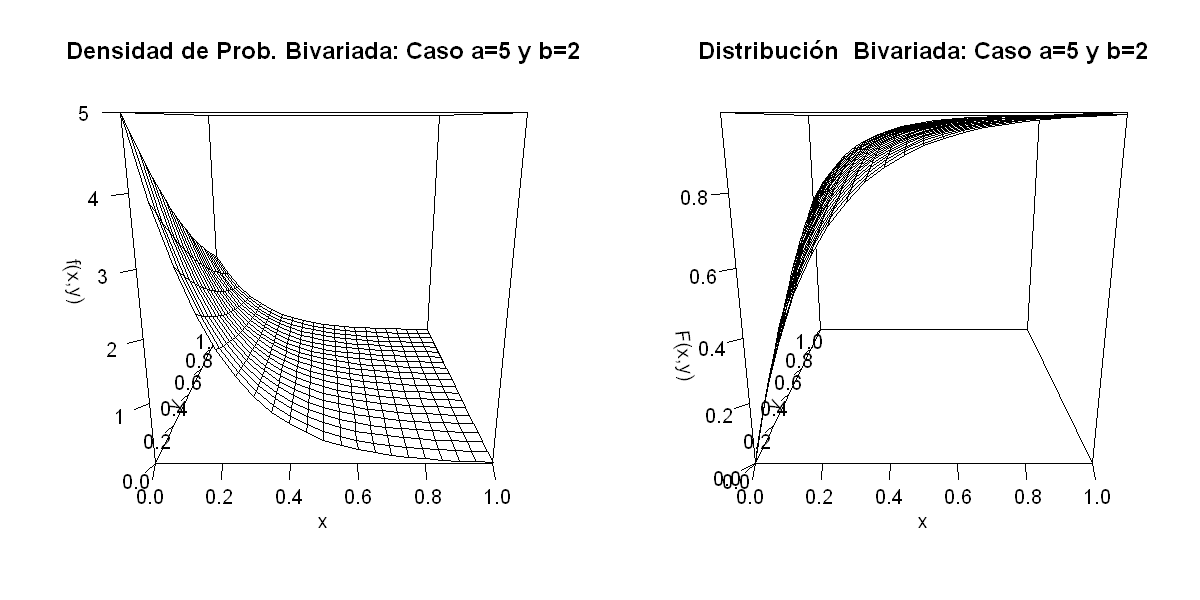
Sea
\(\begin{array}{cl} (X,Y):&\Omega \to \mathbb R_{+}^2\\ &\omega \to (X(\omega),Y(\omega))=(x,y)\\ \end{array}\)
tal que su densidad de probabilidad es:
y entonces la distribución de probabilidad acumulada queda:
Notar que
options(repr.plot.width=10, repr.plot.height=5)
par(mfrow=c(1,2))
x <- seq(0,1,by=0.05)
y <- seq(0,1,by=0.05)
a=5
b=1
dens <- function(x,y) a*b*(exp (-a*x -b*y))
z = outer(x,y,dens)
persp(x,y,z,ticktype = "detailed",zlab="f(x,y)",main="Densidad de Prob. Bivariada: Caso a=5 y b=2")
dist <- function(x,y) 1-exp (-a*x -b*y)
z = outer(x,y,dist)
persp(x,y,z,ticktype = "detailed",zlab="F(x,y)",main="Distribución Bivariada: Caso a=5 y b=2")
2.5. Regla de Bayes¶
En su formulación con variables aleatorias, la regla de Bayes queda:
\(\begin{array}{lll} P(y \mid x)& = & \frac{P(x \mid y) P_Y(y)}{P_X(x)} \,= \, \frac{P(x \mid y) P_Y(y)}{\sum_y P(x\mid y) P_y(y))}\\ \end{array}\)
